Advertisements
Advertisements
Question
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?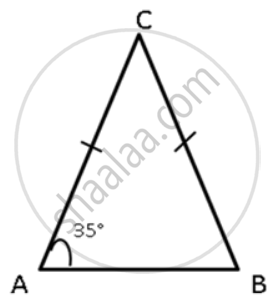
Solution
In ΔABC,
BC = AC ...(given)
⇒ ∠A = ∠B = 35°
Let ∠C = x°
In ΔABC,
∠A + ∠B + ∠C = 180°
35° + 35° + x = 180°
70° + x° = 180°
x° = 180° - 70°
x° = 110°
∠C = x° = 110°
Hence, ∠A = ∠B = 35° and ∠C = 110°
In ΔABC, the greatest angle is ∠C.
As the smallest angles are ∠A and ∠B,
smallest sides are BC and AC.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

How had the position of women improved in our country since independence ? Explain with examples.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.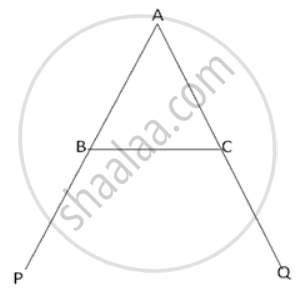
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).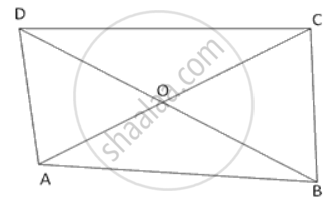
ABCD is a trapezium. Prove that: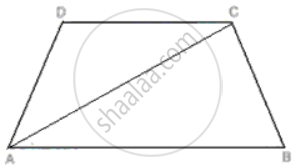
CD + DA + AB > BC.
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT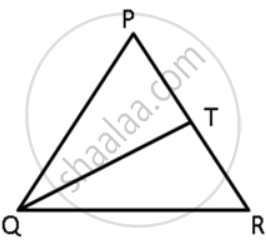
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.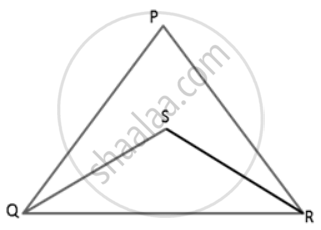
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
