Advertisements
Advertisements
Question
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).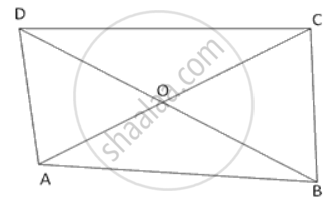
Solution
In ΔAOB, we have
OA + OB > AB ...(i)
In ΔBOC, we have
OB + OC > BC ...(ii)
In ΔCOD, we have
OC + OD > CD ...(iii)
In ΔAOD, we have
OA + OD > AD ....(iv)
Adding (i), (ii), (iii) and (iv), we get
2 (OA + OB + OC + OD) > AB + BC + CD + AD
⇒ 2 [(OA + OC) + (OB + OD)] > AB + BC + CD + AD
⇒ 2 (AC + BD) > AB + BC + CD + AD
[∵ OA + OC = AC and OB + OD = BD]
⇒ AB + BC + CD + AD < 2 (AC + BD).
APPEARS IN
RELATED QUESTIONS
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

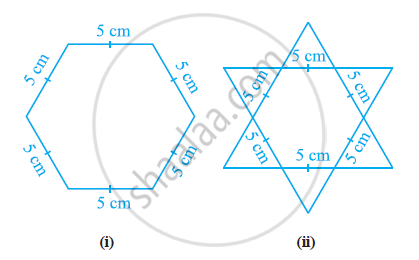
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.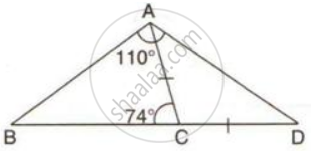
Prove that: BC > CD.
"Caste inequalities are still prevalent in India." Examine the statement.
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Prove that the hypotenuse is the longest side in a right-angled triangle.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS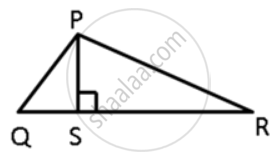
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS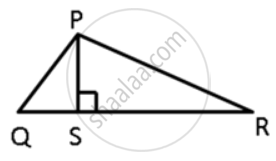
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.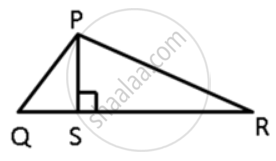
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
