Advertisements
Advertisements
Question
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS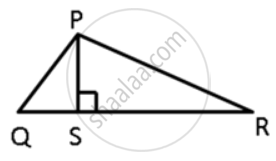
Solution
In ΔPQS,
PS ⊥ QR ....(Given)
PS < PR ....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest.)
I.e. PR > PS.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
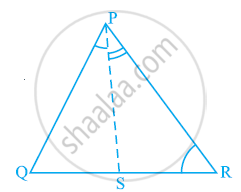
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
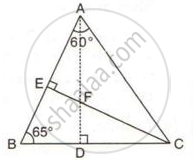
Prove that:
(i) CF > AF
(ii) DC > DF
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
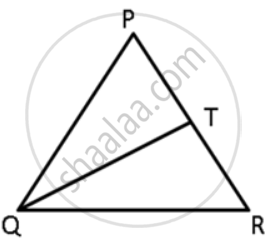
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT