Advertisements
Advertisements
प्रश्न
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS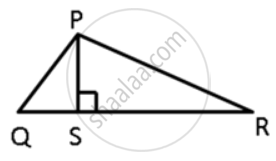
उत्तर
In ΔPQS,
PS ⊥ QR ....(Given)
PS < PR ....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest.)
I.e. PR > PS.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
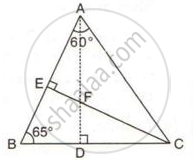
Prove that:
(i) CF > AF
(ii) DC > DF
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.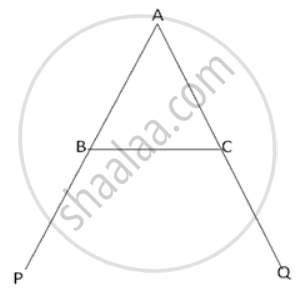
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.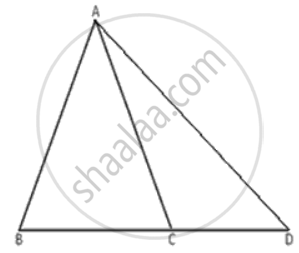
Prove that the hypotenuse is the longest side in a right-angled triangle.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.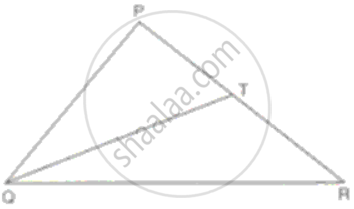
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.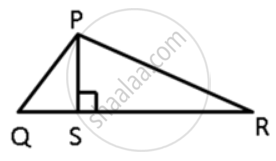
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT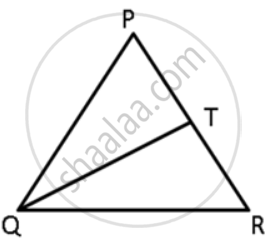
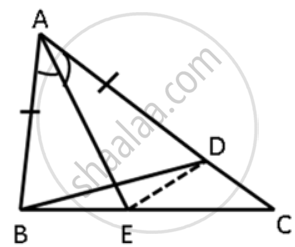
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.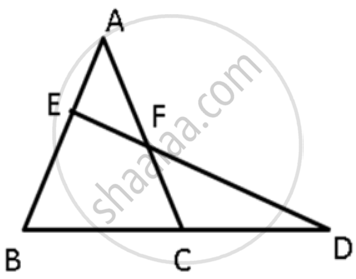
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.