Advertisements
Advertisements
प्रश्न
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS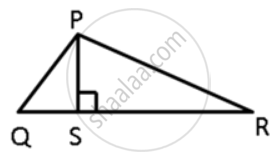
उत्तर
In ΔPQS,
PS < PQ ....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest.)
I.e. PQ > PS
Also, QS < QP ....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest.)
i.e. PQ > QS.
APPEARS IN
संबंधित प्रश्न
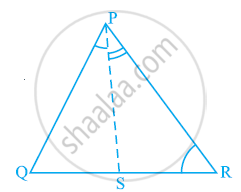
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
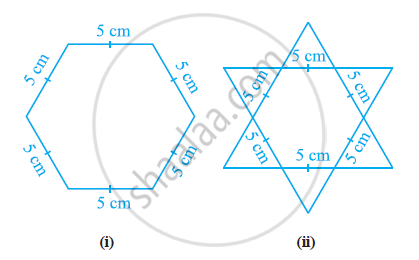
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?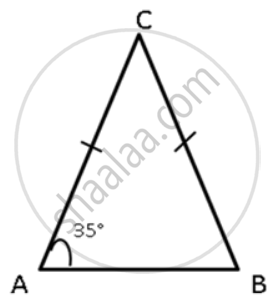
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.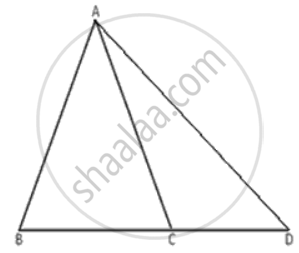
ABCD is a trapezium. Prove that: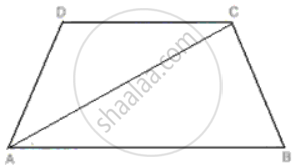
CD + DA + AB + BC > 2AC.
ABCD is a trapezium. Prove that: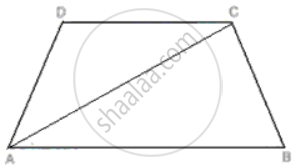
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN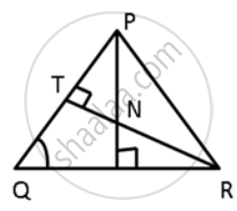
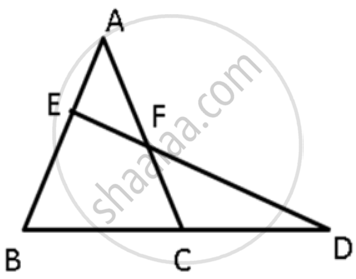
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.