Advertisements
Advertisements
प्रश्न
ABCD is a trapezium. Prove that: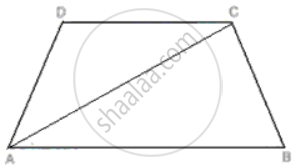
CD + DA + AB > BC.
उत्तर
In ΔACD, we have
CD + DA > CA
⇒ CD + DA + AB > CA +AB
⇒ CD + DA + AB > BC. ...[∴ AB + AC > BC]
APPEARS IN
संबंधित प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.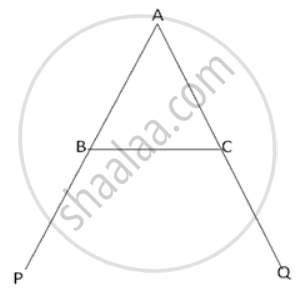
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.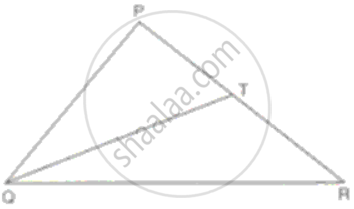
ABCD is a trapezium. Prove that: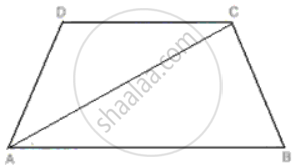
CD + DA + AB + BC > 2AC.
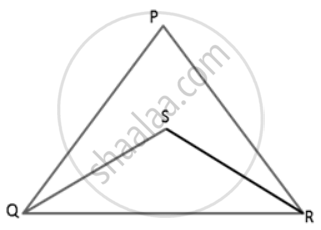
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.