Advertisements
Advertisements
प्रश्न
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.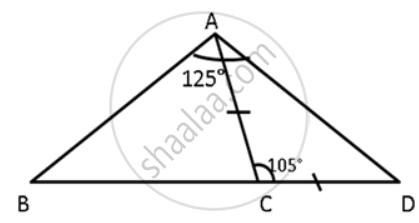
उत्तर
In ΔACD,
AC = CD ....(Given)
∠CDA = ∠DAC ....(ΔACD is isosceles triangle.)
Let ∠CDA = ∠DAC = x°
∠CDA + ∠DAC + ∠ACD = 180°
x° + x° + 105° = 180°
2x° + 180° - 105°
2x° = 75°
x = `(75°)/(2)`
x = 37.5°
∠C = ∠DAC = x° = 37.5° ......(i)
∠DAC =∠AC + ∠BAC
125° - 37.5° = ∠BAC ....from (i)
125° - 37.5° = ∠BAC
87.5° = ∠BAC
Also, ∠BCA + ∠ACD = 180°
⇒ ∠BCA + 105° = 180°
⇒ ∠BCA = 75°
So, in ΔBAC,
∠ACB + ∠BAC + ∠C = 180°
⇒ 75° + 87.5° + ∠ABC = 180°
⇒ ∠ABC = 17.5°
As 87.5° > 17.5°
∠BAC > ∠ABC
⇒ BC > AC
⇒ BC > CD. ....(Since AC = CD)
APPEARS IN
संबंधित प्रश्न
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
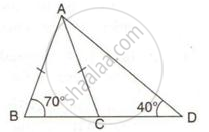
From the following figure, prove that: AB > CD.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.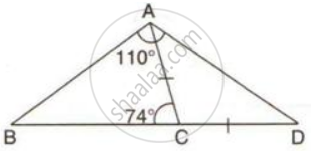
Prove that: BC > CD.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).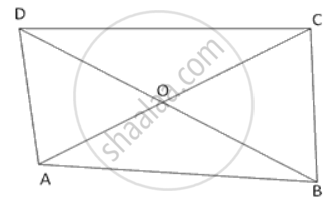
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT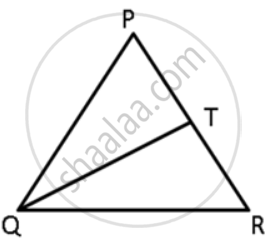
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT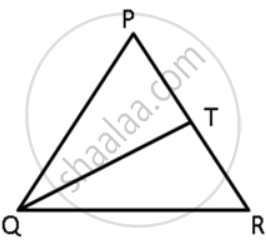
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
