Advertisements
Advertisements
Question
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.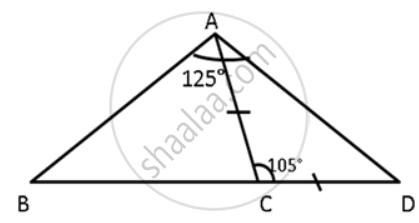
Solution
In ΔACD,
AC = CD ....(Given)
∠CDA = ∠DAC ....(ΔACD is isosceles triangle.)
Let ∠CDA = ∠DAC = x°
∠CDA + ∠DAC + ∠ACD = 180°
x° + x° + 105° = 180°
2x° + 180° - 105°
2x° = 75°
x = `(75°)/(2)`
x = 37.5°
∠C = ∠DAC = x° = 37.5° ......(i)
∠DAC =∠AC + ∠BAC
125° - 37.5° = ∠BAC ....from (i)
125° - 37.5° = ∠BAC
87.5° = ∠BAC
Also, ∠BCA + ∠ACD = 180°
⇒ ∠BCA + 105° = 180°
⇒ ∠BCA = 75°
So, in ΔBAC,
∠ACB + ∠BAC + ∠C = 180°
⇒ 75° + 87.5° + ∠ABC = 180°
⇒ ∠ABC = 17.5°
As 87.5° > 17.5°
∠BAC > ∠ABC
⇒ BC > AC
⇒ BC > CD. ....(Since AC = CD)
APPEARS IN
RELATED QUESTIONS
In the following figure, write BC, AC, and CD in ascending order of their lengths.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS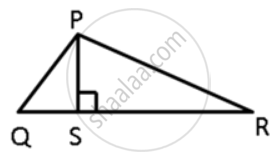
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS