Advertisements
Advertisements
Question
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Solution
In the given ΔDEF the greatest angle is ∠F and
the opposite side to the ∠F is DE
Hence, the greatest side is DE.
The smallest angle in the ΔDEF is D and the opposite
side to the ∠D is EF.
Hence, the smallest side is EF.
APPEARS IN
RELATED QUESTIONS
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.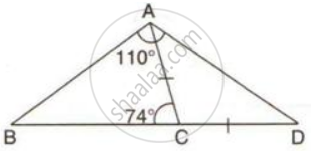
Prove that: BC > CD.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.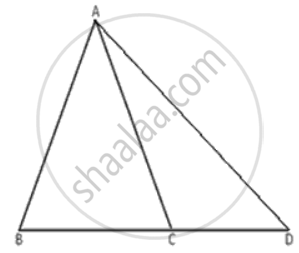
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
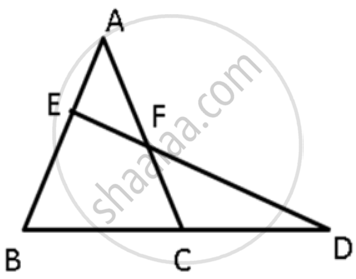
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.