Advertisements
Advertisements
प्रश्न
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
उत्तर
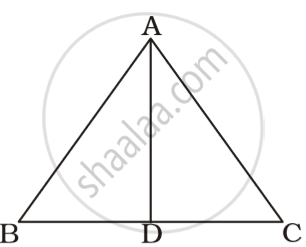
In ΔADC
AD > AC
⇒ ∠ACD > ∠ADC ...(i)
In ΔABD
∠ABD + ∠BAD = ∠ADC ...(ii)
Putting the value of ∠ADC in equation (i)
∠ACD > ∠ABD + ∠BAD ...(iii)
⇒ ∠ACD > ∠ABD
⇒ ∠ACB > ∠ABC
AB > AC
APPEARS IN
संबंधित प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
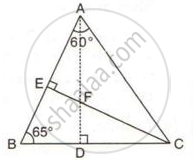
Prove that:
(i) CF > AF
(ii) DC > DF
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?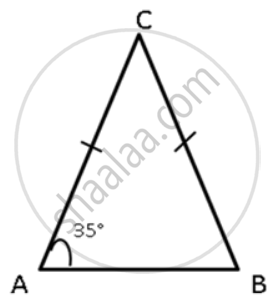
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.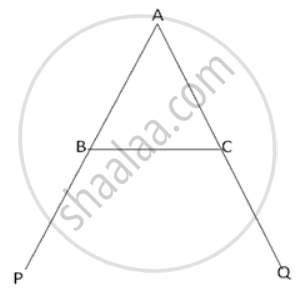
Prove that the hypotenuse is the longest side in a right-angled triangle.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
