Advertisements
Advertisements
प्रश्न
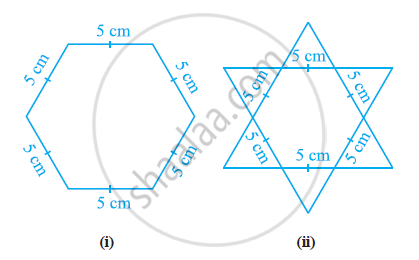
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
उत्तर
It can be observed that hexagonal-shaped rangoli has 6 equilateral triangles in it.
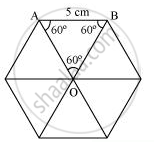
`"Area of "ΔOAB = sqrt3/4"(side)"^2`
`= sqrt3/4(5)^2`
`= sqrt3/4(25)`
`= (25sqrt3)/4cm^2`
`"Area of hexagonal-shaped rangoli "=6xx(25sqrt3)/4=(75sqrt3)/2cm^2`
`"Area of equilateral triangle having its side as 1cm "=sqrt3/4(1)^2=sqrt3/4cm^2`
`"Number of equilateral triangles of 1 cm side that can be filled in this hexagonal-shaped rangoli "=((75sqrt3)/2)/(sqrt3/4)=150`
Star-shaped rangoli has 12 equilateral triangles of side 5 cm in it.
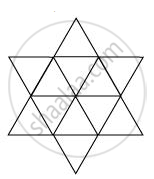
`"Area of star-shaped rangoli "=12xxsqrt3/4xx(5)^2=75sqrt3`
`"Number of equilateral triangles of 1 cm side that can be filled in this star-shaped rangoli "=(75sqrt3)/(sqrt3/4)=300`
Therefore, star-shaped rangoli has more equilateral triangles in it.
APPEARS IN
संबंधित प्रश्न
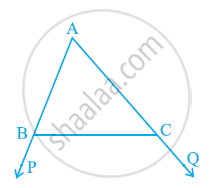
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
In the following figure, write BC, AC, and CD in ascending order of their lengths.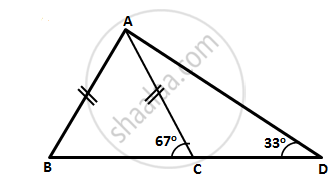
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.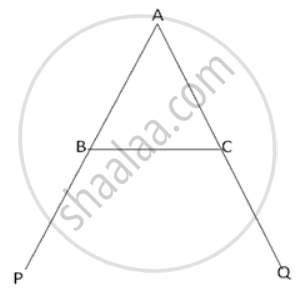
Prove that the perimeter of a triangle is greater than the sum of its three medians.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS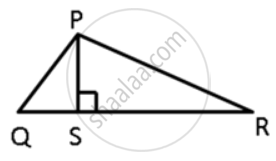
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
