Advertisements
Advertisements
प्रश्न
Prove that the perimeter of a triangle is greater than the sum of its three medians.
उत्तर
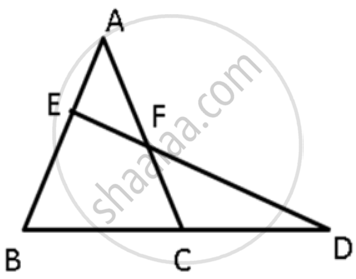
Given: A ΔABC ion which AD, BE and CF are its medians.
To Prove: we know that the sum of any two dies of a triangle is greater than twice the median bisecting the third side. Therefore,
AD is the median bisecting BC
⇒ AB + AC > 2AD ...(i)
BE is the median bisecting AC ...(ii)
And, CF is the median bisecting AB
⇒ BC + AC > 2EF ...(iii)
Adding (i), (ii) and (iii), we get
(AB + AC) + (AB + BC) + (BC + AC) > 2. AD + 2. BE + 2. BE + 2. CF
⇒ 2 (AB + BC + AC) > 2 (AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF.
APPEARS IN
संबंधित प्रश्न
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
How had the position of women improved in our country since independence ? Explain with examples.
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
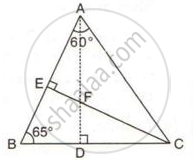
Prove that:
(i) CF > AF
(ii) DC > DF
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
ABCD is a trapezium. Prove that: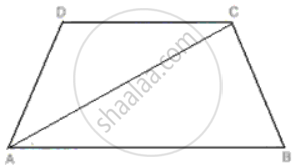
CD + DA + AB + BC > 2AC.
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.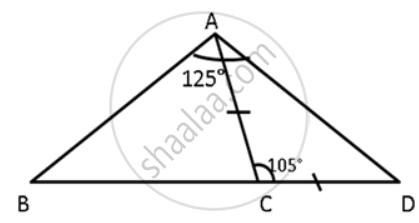
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.