Advertisements
Advertisements
Question
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Solution
Given: A ΔABC ion which AD, BE and CF are its medians.
To Prove: we know that the sum of any two dies of a triangle is greater than twice the median bisecting the third side. Therefore,
AD is the median bisecting BC
⇒ AB + AC > 2AD ...(i)
BE is the median bisecting AC ...(ii)
And, CF is the median bisecting AB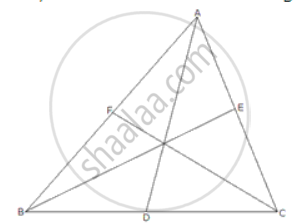
⇒ BC + AC > 2EF ...(iii)
Adding (i), (ii) and (iii), we get
(AB + AC) + (AB + BC) + (BC + AC) > 2. AD + 2. BE + 2. BE + 2. CF
⇒ 2 (AB + BC + AC) > 2 (AD + BE + CF)
⇒ AB + BC + AC > AD + BE + CF.
APPEARS IN
RELATED QUESTIONS
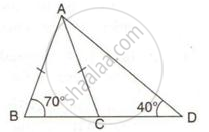
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
From the following figure, prove that: AB > CD.
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
Prove that the hypotenuse is the longest side in a right-angled triangle.
ABCD is a trapezium. Prove that: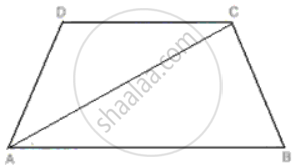
CD + DA + AB + BC > 2AC.
ABCD is a trapezium. Prove that: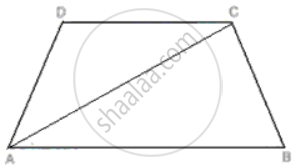
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN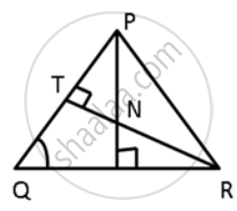
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR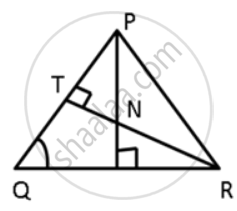
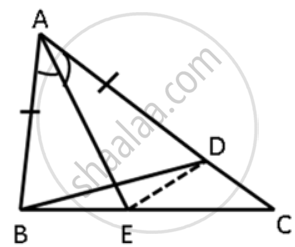
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.