Advertisements
Advertisements
Question
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Solution
The sum of any two sides of the triangle is always greater than third side of the triangle.
Third side < 13 + 8 = 21 cm.
The difference between any two sides of the triangle is always less than the third side of the triangle.
Third side > 13 - 8 = 5 cm.
Therefore, the length of the third side is between 5 cm and 21 cm, respectively.
The value of a = 5 cm and b = 21cm.
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
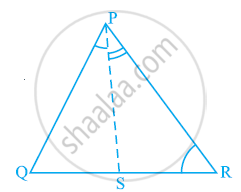
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
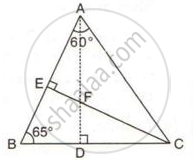
Prove that:
(i) CF > AF
(ii) DC > DF
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
Prove that the perimeter of a triangle is greater than the sum of its three medians.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN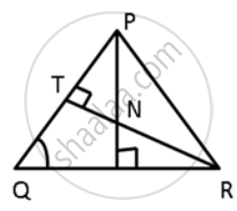
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR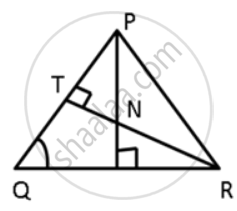
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS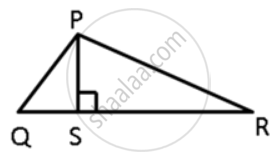
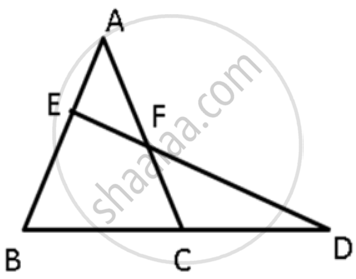
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.