Advertisements
Advertisements
प्रश्न
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR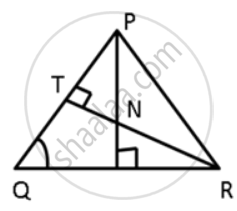
उत्तर
In ΔRTQ,
∠RTQ + ∠TQR + ∠TRQ = 180°
90° + 60° +∠TRQ = 180°
150° + ∠TRQ = 180°
∠TRQ = 180° - 150°
∠TRQ = 30°
∠TRQ = ∠SRN = 30° ....(i)
In NSR,
∠RNS + ∠SRN = 90° ....(∵∠NSR = 90°)
∠RNS + 30° = 90° ....[from (iii)]
∠RNS = 90° - 30°
∠RNS = 60° ....(ii)
∠SRN < ∠RNS ....(from (iii) and (iv))
SN < SR.
APPEARS IN
संबंधित प्रश्न
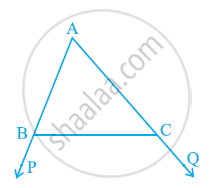
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
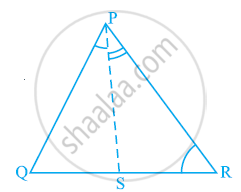
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
How had the position of women improved in our country since independence ? Explain with examples.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.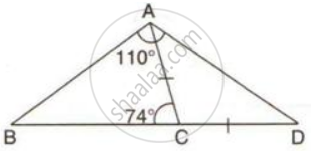
Prove that: BC > CD.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.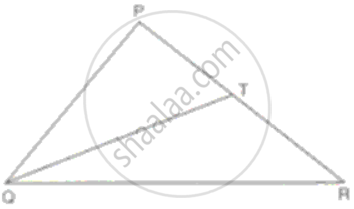
ABCD is a trapezium. Prove that: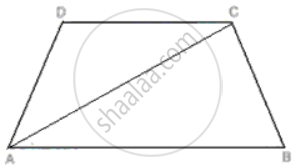
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN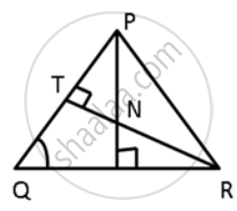
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.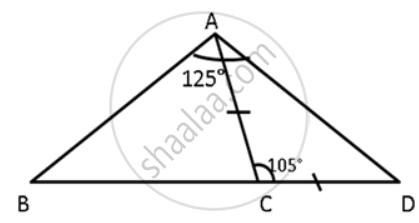
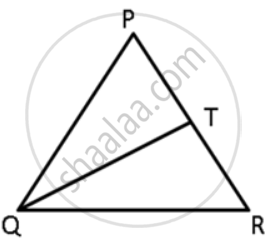
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT