Advertisements
Advertisements
प्रश्न
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT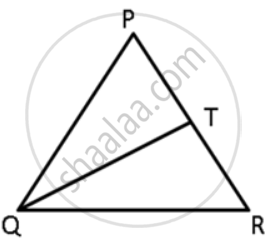
उत्तर
In ΔPQR,
PQ = QR = PR
⇒ ∠P = Q = ∠ = 60°
In ΔPQT,
∠PQT < 60°
∴ ∠PQT < ∠P
∴ PT < QT.
APPEARS IN
संबंधित प्रश्न
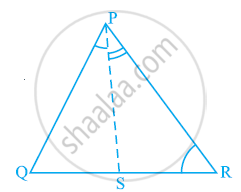
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
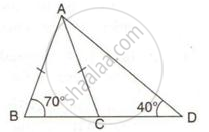
From the following figure, prove that: AB > CD.
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.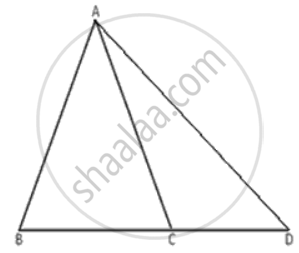
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.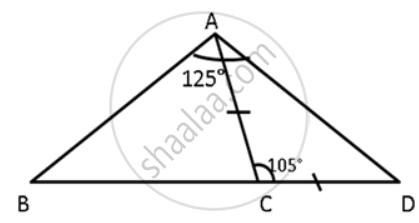
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT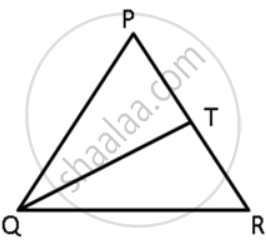
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.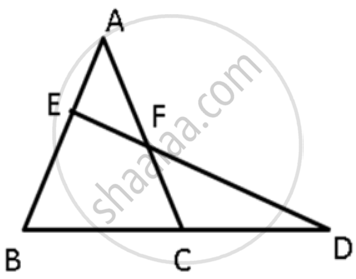
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
