Advertisements
Advertisements
प्रश्न
From the following figure, prove that: AB > CD.
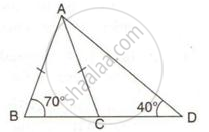
उत्तर
In ΔABC,
AB = AC ...[ Given ]
∴ ∠ACB = ∠B ...[ angles opposite to equal sides are equal ]
∠B = 70° ...[ Given ]
⇒ ∠ACB = 70° ...(i)
Now,
∠ACB +∠ACD = 180°...[ BCD is a straight line]
⇒ 70° + ∠ACD = 180°
⇒ ∠ACD = 110° ...(ii)
In ΔACD,
∠CAD + ∠ACD + ∠D = 180°
⇒ ∠CAD + 110° + ∠D = 180° ...[ From (ii) ]
⇒ ∠CAD + ∠D = 70°
But ∠D = 40° ...[ Given ]
⇒ ∠CAD + 40°= 70°
⇒ ∠CAD = 30° …(iii)
In ΔACD,
∠ACD = 110° ...[ From (ii) ]
∠CAD = 30° ...[ From (iii) ]
∠D = 40° ...[ Given ]
∴ D > ∠CAD
⇒ AC > CD ....[Greater angle has greater side opposite to it]
Also,
AB = AC ...[ Given ]
Therefore, AB > CD.
APPEARS IN
संबंधित प्रश्न
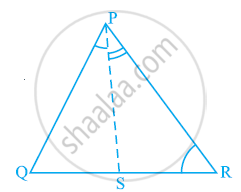
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
How had the position of women improved in our country since independence ? Explain with examples.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).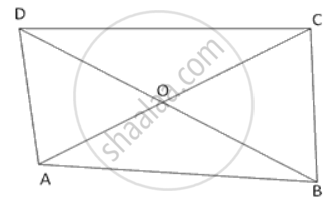
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.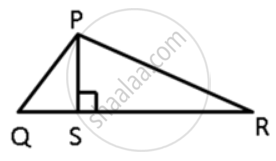
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.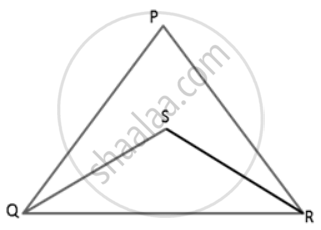
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
