Advertisements
Advertisements
प्रश्न
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
उत्तर
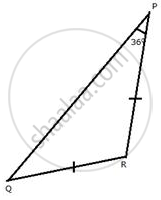
In ΔPQR,
QR = PR ...[ Given ]
∴ ∠P = ∠Q ...[ angles opposite to equal sides are equal ]
⇒ ∠P = 36° ..[Given]
⇒ ∠Q = 36°
In ΔPQR,
∠P + ∠Q + ∠R = 180°
⇒ 36° + 36° + ∠R = 180°
⇒ ∠R + 72° = 180°
⇒ ∠R = 108°
Now,
∠R = 108°
∠P = 36°
∠Q = 36°
Since ∠R is the greatest, therefore, PQ is the largest side.
APPEARS IN
संबंधित प्रश्न
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.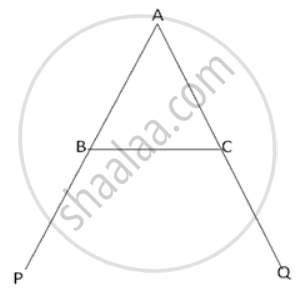
Prove that the perimeter of a triangle is greater than the sum of its three medians.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).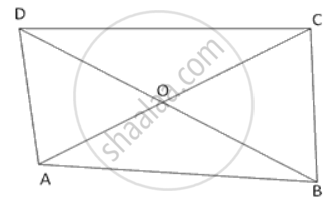
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS
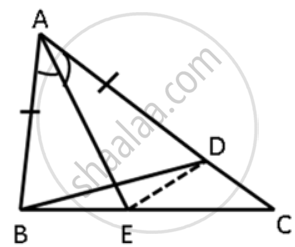
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.