Advertisements
Advertisements
प्रश्न
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
उत्तर
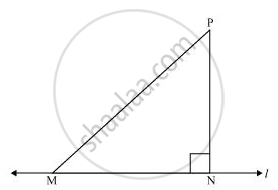
Let us take a line l and from point P (i.e., not on line l), draw two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.
In ΔPNM,
∠N = 90º
∠P + ∠N + ∠M = 180º (Angle sum property of a triangle)
∠P + ∠M = 90º
Clearly, ∠M is an acute angle.
∴ ∠M < ∠N
⇒ PN < PM (Side opposite to the smaller angle is smaller)
Similarly, by drawing different line segments from P to l, it can be proved that PN is smaller in comparison to them.
Therefore, it can be observed that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
APPEARS IN
संबंधित प्रश्न
How had the position of women improved in our country since independence ? Explain with examples.
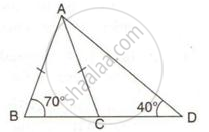
From the following figure, prove that: AB > CD.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.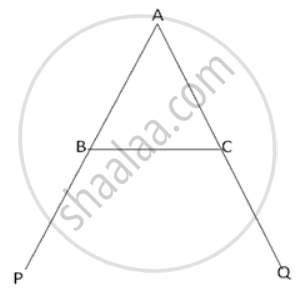
Prove that the perimeter of a triangle is greater than the sum of its three medians.
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
