Advertisements
Advertisements
प्रश्न
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
उत्तर
In triangle APR,
AP + AR > PR ......(i)
In triangle BPQ,
BQ + PB > PQ .......(ii)
In triangle QCR,
QC + CR > QR .......(iii)
Adding (i), (ii) and (iii)
AP + AR + BQ + PB + QC + CR > PR + PQ + QR
(AP + PB) + (BQ + QC) + (CR + AR) > PR + QR + PQ)
⇒ AB + BC + AC > PQ + QR + PR.
APPEARS IN
संबंधित प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
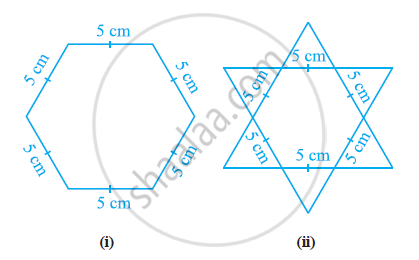
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS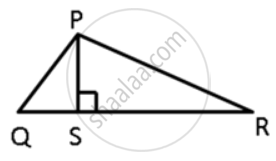
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.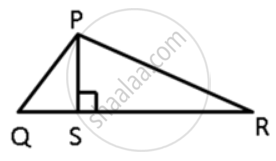
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.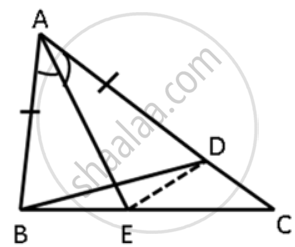
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
