Advertisements
Advertisements
प्रश्न
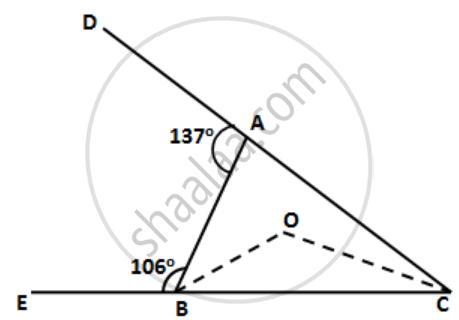
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
उत्तर

∠BAC = 180° - ∠BAD = 180° - 137° = 43°
∠ABC = 180° - ∠ABE = 180° - 106° = 74°
Thus, in ΔABC,
∠ACB = 180° - ∠BAC - ∠ABC
⇒ ∠ACB = 180° - 43° - 74° = 63°
Now, ∠ABC = ∠OBC + ∠ABO
⇒ ∠ABC = 2∠OBC ....( OB is biosector of ∠ABC )
⇒ 74° = 2∠OBC
⇒ ∠OBC = 37°
Similarly,
∠ACB = ∠OCB + ∠ACO
⇒ ∠ACB = 2∠OCB ...( OC is bisector of ACB )
⇒ 63° = 2∠OCB
⇒ ∠OCB = 31.5°
Now, in ΔBOC,
∠BOC = 180° - ∠OBC - ∠OCB
⇒ ∠BOC = 180° - 37° - 31.5°
⇒ ∠BOC = 111.5°
Since, ∠BOC> ∠OBC > ∠OCB, we have
BC > OC > OB
APPEARS IN
संबंधित प्रश्न
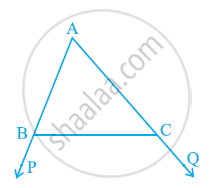
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

From the following figure, prove that: AB > CD.
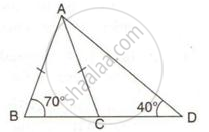
In the following figure, write BC, AC, and CD in ascending order of their lengths.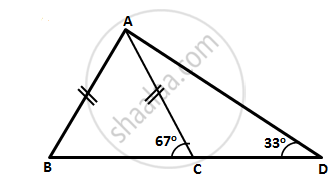
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
ABCD is a trapezium. Prove that: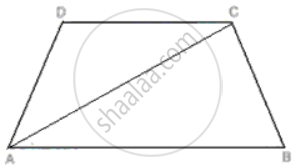
CD + DA + AB > BC.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS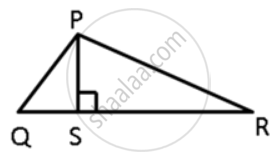
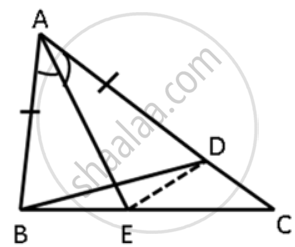
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.