Advertisements
Advertisements
Question
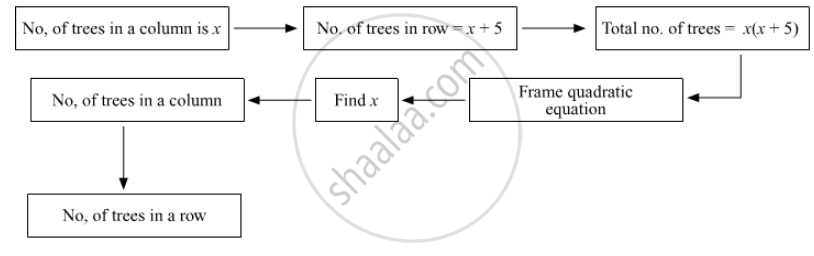
In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of following flow chart.

Solution
Let the number of trees in each column be x.
Number of trees in a row = x + 5
Total trees = Number of rows \[\times\] Number of columns = \[x\left( x + 5 \right)\] =150
\[\Rightarrow x\left( x + 5 \right) = 150\]
\[ \Rightarrow x^2 + 5x - 150 = 0\]
\[ \Rightarrow x^2 + 15x - 10x - 150 = 0\]
\[ \Rightarrow x\left( x + 15 \right) - 10\left( x + 15 \right) = 0\]
\[ \Rightarrow \left( x + 15 \right)\left( x - 10 \right) = 0\]
\[ \Rightarrow x = 10, - 15\]
But number of columns cannot be negative so, number of columns = 10.
Number of rows = 10 + 5 = 15
APPEARS IN
RELATED QUESTIONS
The sum of two natural numbers is 8 and their product is 15., Find the numbers.
Find the solution of the quadratic equation `3sqrt3x^2+10x+sqrt3=0`
If the roots of the quadratic equation `2x^2+8x+k=0` are equal then find the value of k.
If the quadratic equation `px^2-2sqrt5px+15=0` has two equal roots then find the value of p.
Find the value of k so that the quadratic equation` x^2-4kx+k=0`
has equal roots.
Solve `x^2-(sqrt3+1)x+sqrt3=0`
Write the following equation in the form ax2 + bx + c = 0, then write the values of a, b, c for the equation.
(x – 1)2 = 2x + 3
The Sum of squares of 2 consecutive natural even numbers is 244; find the numbers.
Choose the correct answer for the following question.
The roots of x2 + kx + k = 0 are real and equal, find k.
Choose the correct answer for the following question.
One of the roots of equation x2 + mx – 5 = 0 is 2; find m.
Is the following equation quadratic?
x2 - 2x + 5 = x2
Solve the following quadratic equation.
`1/(x + 5) = 1/x^2`
Which of the following is a quadratic equation ?
Two water taps together can fill a tank in `1 7/8` hours. The tap with a longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Write the quadratic equation 7 = 4x - x2 in the form of ax2+bx + c = 0.
In an orchard there are total 200 trees. If the number of trees in each column is more by 10 than the number of trees in each row, then find the number of trees in each row
Form a quadratic equation such that one of its roots is 5. Form a quadratic equation for it and write. (For the formation of word problems you can use quantities like age, rupees, or natural numbers.) (Sample solution for the above example is given below students can take another number to form another example)
Solution:
We need one of the solutions of the quadratic equation as 5.
Then we can take another root as any number like a positive or negative number or zero. Here I am taking another root of the quadratic equation as 2.
Then we can form a word problem as below,
Smita is younger than her sister Mita by 3 years (5 – 2 = 3). If the product of their ages is (5 × 2 = 10). Then find their present ages.
Let the age of Mita be x.
Therefore age of Smita = x – 3
By the given condition,
x(x – 3) = 10
x2 – 3x – 10 = 0
Let p and q be two positive numbers such that p + q = 2 and p4 + q4 = 272. Then p and q are roots of the equation ______.
