Balbharati solutions for Algebra (Mathematics 1) [English] 10 Standard SSC Maharashtra State Board chapter 2 - Quadratic Equations [Latest edition]

Write any two quadratic equations.

Decide whether the following equation is quadratic equation or not.

x² + 5x – 2 = 0

Decide whether the following equation is quadratic equation or not.

 y² = 5y – 10

Decide whether the following equation is quadratic equation or not.

`"y"^2 + 1/"y" = 2`

Decide whether the following equation is quadratic equation or not.

\[x + \frac{1}{x} = - 2\] 

Decide whether the following equation is quadratic equation or not.

(m + 2) (m – 5) = 0

Decide whether the following equation is quadratic equation or not.

 m³ + 3m² – 2 = 3m³

Write the following equation in the form ax² + bx + c = 0, then write the values of a, b, c for the equation.  

2y = 10 – y²

Write the following equation in the form ax² + bx + c = 0, then write the values of a, b, c for the equation.

 (x – 1)² = 2x + 3

Write the following equation in the form ax² + bx + c= 0, then write the values of a, b, c for the equation.

x² + 5x = –(3 – x)

Write the following equation in the form ax² + bx + c= 0, then write the values of a, b, c for the equation.

3m² = 2m² – 9

Write the following equation in the form ax² + bx + c= 0, then write the values of a, b, c for equation. 

P(3+6p) = –5 

Write the following equation in the form ax² + bx + c= 0, then write the values of a, b, c for the equation.

x² – 9 = 13

Determine whether the values given against the quadratic equation are the roots of the equation.

x² + 4x – 5 = 0 , x = 1, –1

Determine whether the values given against the quadratic equation are the roots of the equation.

2m² – 5m = 0, m = 2, `5/2`

Find k if x = 3 is a root of equation kx² – 10x + 3 = 0.

One of the roots of equation 5m² + 2m + k = 0 is `(-7)/5` Complete the following activity to find the value of 'k'.

Solve the following quadratic equation by factorisation.

 x² – 15x + 54 = 0

Solve the following quadratic equation by factorisation.

x² + x – 20 = 0

Solve the following quadratic equation by factorisation.

 2y² + 27y + 13 = 0

Solve the following quadratic equation by

factorisation.

5m² = 22m + 15

Solve the following quadratic equation by factorization.

`2"x"^2 - 2"x" + 1/2 = 0`

Solve the following quadratic equation by factorisation.

\[6x - \frac{2}{x} = 1\]

Solve the following quadratic equation by factorisation.

`sqrt2 x^2 + 7x + 5sqrt2 = 0`  to solve this quadratic equation by factorisation, complete the following activity.

`sqrt2 x^2 + 7x + 5sqrt2 = 0`

`sqrt2x^2+square+square+5sqrt2=0` 

`x("______") + sqrt2 ("______") = 0`

(______) (x + 2) = 0

(______) = 0 or (x + 2) = 0

∴ x = `square` or x = - 2

∴ `square` and `sqrt(-2)` are roots of the equation.

Solve the following quadratic equation by factorisation.
3x² - 2√6x + 2 = 0

Solve the following quadratic equation by factorisation.

2m (m − 24) = 50

Solve the following quadratic equation by factorisation.

\[25 m^2 = 9\]

Solve the following quadratic equation by factorisation.

7m² = 21m

Solve the following quadratic equation by factorisation.

m² - 11 = 0

Solve the following quadratic equation by completing the square method.

x² + x – 20 = 0

Solve the following quadratic equation by completing the square method.

x² + 2x – 5 = 0

Solve the following quadratic equation by completing the square method.

 m² – 5m = –3

Solve the following quadratic equation by completing the square method.

9y² – 12y + 2 = 0

Solve the following quadratic equation by completing the square method.

 2y² + 9y + 10 = 0

Solve the following quadratic equation by completing the square method.

5x² = 4x + 7

Compare the given quadratic equation to the general form and write values of a, b, c.

x² – 7x + 5 = 0

Compare the given quadratic equation to the general form and write values of a,b, c.

2m² = 5m – 5

Compare the given quadratic equation to the general form and write values of a,b, c.

y² = 7y

Solve using formula.

x² + 6x + 5 = 0

Solve using formula.

x² – 3x – 2 = 0

Solve using formula.

3m² + 2m – 7 = 0

Solve using formula.

5m² – 4m – 2 = 0

Solve using formula.

y² + `1/3`y = 2.

Solve using formula.

5x² + 13x + 8 = 0

With the help of the flow chart given below solve the equation \[x^2 + 2\sqrt{3}x + 3 = 0\] using the formula.

Fill in the gaps and complete. 

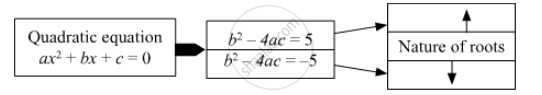
Fill in the gap and complete. 

Fill in the gaps and complete.

If α, β are roots of quadratic equation, 

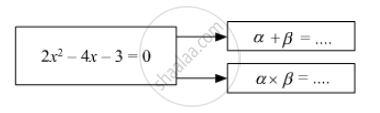
Find the value of discriminant.  

 x² + 7x – 1 = 0 

Find the value of discriminant. 

 2y² – 5y + 10 = 0

Find the value of discriminant. 

`sqrt2x^2 + 4x + 2sqrt2 = 0`

Determine the nature of roots of the following quadratic equation.

 x² – 4x + 4 = 0

Determine the nature of roots of the following quadratic equation.

 2y² – 7y + 2 = 0

Determine the nature of roots of the following quadratic equation.

m² + 2m + 9 = 0

Form the quadratic equation from the roots given below.

 0 and 4

Form the quadratic equation from the roots given below.

 3 and –10

Form the quadratic equation from the roots given below.

\[\frac{1}{2}, - \frac{1}{2}\]

Form the quadratic equation from the roots given below.

\[2 - \sqrt{5}, 2 + \sqrt{5}\]

Sum of the roots of a quadratic equation is double their product. Find k if equation x² – 4kx + k + 3 = 0

α, β are roots of y² – 2y –7 = 0 find, 

α² + β² 

α, β are roots of y² – 2y –7 = 0 find, 

α³ + β³ 

The roots of the following quadratic equation is real and equal, find k.

3y² + ky +12 = 0

The roots of the following quadratic equation is real and equal, find k.

 kx (x – 2) + 6 = 0

Product of Pragati’s age 2 years ago and 3 years hence is 84. Find her present age. 

The Sum of squares of 2 consecutive natural even numbers is 244; find the numbers.

In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of following flow chart. 

Vivek is older than Kishor by 5 years. The sum of the reciprocals of their ages is \[\frac{1}{6}\] Find their present ages. 

Suyash scored 10 marks more in second test than that in the first. 5 times the score of the second test is the same as square of the score in the first test. Find his score in the first test.

Mr. Kasam runs a small business of making earthen pots. He makes certain number of pots on daily basis. Production cost of each pot is Rs 40 more than 10 times total number of pots, he makes in one day. If production cost of all pots per day is Rs 600, find production cost of one pot and number of pots he makes per day.

Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of boat in still water is 12 km. per hour. Find the speed of water current. 

Pintu takes 6 days more than those of Nishu to complete certain work. If they work together they finish it in 4 days. How many days would it take to complete the work if they work alone. 

If 460 is divided by a natural number, quotient is 6 more than five times the divisor and remainder is 1. Find quotient and divisor.

In the adjoining fig. `square` ABCD is a trapezium AB || CD and its area is 33 cm². From the information given in the figure find the lengths of all sides of the `square` ABCD. Fill in the empty boxes to get the solution.

Solution: `square` ABCD is a trapezium.

AB || CD

`"A"(square "ABCD") = 1/2 ("AB" + "CD") xx`______

33 = `1/2 ("x" + 2"x" + 1) xx `______

∴ ______ = (3x + 1) × ______

∴ 3x² +______ − ______ = 0

∴ 3x(______) + 10(______) = 0

∴ (3x + 10) (______) = 0

∴ (3x + 10) = 0 or ______ = 0

∴ x = `-10/3` or x = ______

But length is never negative.

∴ `"x" ≠ -10/3`

∴ x = ______

AB = ______, CD = ______, AD = BC = ______

Which one is the quadratic equation?

Choose the correct answer for the following question.
Out of the following equations which one is not a quadratic equation?

Choose the correct answer for the following question.

The roots of x² + kx + k = 0 are real and equal, find k.

Choose the correct answer for the following question.
For \[\sqrt{2} x^2 - 5x + \sqrt{2} = 0\] find the value of the discriminant.

Choose the correct answer for the following question.
Which of the following quadratic equations has roots 3,5?

Choose the correct answer for the following question.

Out of the following equations, find the equation having the sum of its roots –5.

Choose the correct answer for the following question.

\[\sqrt{5} m^2 - \sqrt{5}m + \sqrt{5} = 0\] which of the following statement is true for this given equation?

Choose the correct answer for the following question.

One of the roots of equation x² + mx – 5 = 0 is 2; find m.

Which is the following equation quadratic?

x² + 2x + 11 = 0

Is the following equation quadratic?

x² - 2x + 5 = x²

is the following equation quadratic?

\[\left( x + 2 \right)^2 = 2 x^2\] 

Find the value of discriminant of the following equation.

2y² − y + 2 = 0

Find the value of discriminant of the following equation.

5m² - m = 0

Find the value of discriminant of the following equation.

\[\sqrt{5} x^2 - x - \sqrt{5} = 0\]

One of the roots of quadratic equation \[2 x^2 + kx - 2 = 0\] is –2. find k.

Two roots of quadratic equation is given ; frame the equation.

 10 and –10

Two roots of quadratic equation is given ; frame the equation.

\[1 - 3\sqrt{5} \text{ and } 1 + 3\sqrt{5}\] 

Two roots of quadratic equation is given ; frame the equation.

 0 and 7

Determine the nature of root of the quadratic equation.

\[3 x^2 - 5x + 7 = 0\]

Determine the nature of root of the quadratic equation.

\[\sqrt{3} x^2 + \sqrt{2}x - 2\sqrt{3} = 0\]

Determine the nature of root of the quadratic equation.

m² - 2m + 1 = 0

Solve the following quadratic equation.

`1/(x + 5) = 1/x^2`

Solve the following quadratic equation.

\[x^2 - \frac{3x}{10} - \frac{1}{10} = 0\]

Solve the following quadratic equation.

(2x + 3)² = 25

Solve the following quadratic equation.

m² + 5m + 5 = 0

Solve the following quadratic equation.

5m² + 2m + 1 = 0

Solve the following quadratic equation.

x² - 4x - 3 = 0

Find m if (m – 12) x² + 2(m – 12) x + 2 = 0 has real and equal roots.

The sum of two roots of a quadratic equation is 5 and sum of their cubes is 35, find the equation.

Find quadratic equation such that its roots are square of sum of the roots and square of difference of the roots of equation \[2 x^2 + 2\left( p + q \right)x + p^2 + q^2 = 0\]

The difference between squares of two numbers is 120. The square of smaller number is twice the greater number. Find the numbers. 

Ranjana wants to distribute 540 oranges among some students. If 30 students were more each would get 3 oranges less. Find the number of students.

Mr. Dinesh owns an agricultural farm at village Talvel. The length of the farm is 10 meter more than twice the breadth. In order to harvest rain water, he dug a square shaped pond inside the farm. The side of pond is `1/3` of the breadth of the farm. The area of the farm is 20 times the area of the pond. Find the length and breadth of the farm and of the pond. 

A tank fills completely in 2 hours if both the taps are open. If only one of the taps is open at the given time, the smaller tap takes 3 hours more than the larger one to fill the tank. How much time does each tap take to fill the tank completely?