Advertisements
Advertisements
Question
Solve the following quadratic equation by completing the square method.
9y2 – 12y + 2 = 0
Solution
9y2 – 12y + 2 = 0
\[\Rightarrow y^2 - \frac{12}{9}y + \frac{2}{9} = 0\]
\[ \Rightarrow y^2 - \frac{4}{3}y + \frac{2}{9} = 0\]
\[ \Rightarrow y^2 - \frac{4}{3}y + \left( \frac{\frac{4}{3}}{2} \right)^2 - \left( \frac{\frac{4}{3}}{2} \right)^2 + \frac{2}{9} = 0\]
\[ \Rightarrow y^2 - \frac{4}{3}y + \left( \frac{2}{3} \right)^2 - \left( \frac{2}{3} \right)^2 + \frac{2}{9} = 0\]
\[\Rightarrow \left[ y^2 - \frac{4}{3}y + \left( \frac{4}{9} \right) \right] - \left( \frac{4}{9} \right) + \frac{2}{9} = 0\]
\[ \Rightarrow \left( y - \frac{2}{3} \right)^2 - \frac{2}{9} = 0\]
\[ \Rightarrow \left( y - \frac{2}{3} \right)^2 = \frac{2}{9}\]
\[ \Rightarrow \left( y - \frac{2}{3} \right)^2 = \left( \frac{\sqrt{2}}{3} \right)^2 \]
\[\Rightarrow y - \frac{2}{3} = \frac{\sqrt{2}}{3} \text{ or } y - \frac{2}{3} = - \frac{\sqrt{2}}{3}\]
\[ \Rightarrow y = \frac{\sqrt{2}}{3} + \frac{2}{3} \text{ or } y = - \frac{\sqrt{2}}{3} + \frac{2}{3}\]
\[ \Rightarrow y = \frac{\sqrt{2} + 2}{3} \text{ or } y = \frac{- \sqrt{2} + 2}{3}\]
APPEARS IN
RELATED QUESTIONS
Solve the following quadratic equation by completing square method : x2 + 10x + 21 = 0.
Find the roots of the quadratic equations `4x^2+4sqrt3x + 3 = 0` by applying the quadratic formula.
Find the roots of the following equations:
`x-1/x = 3, x ≠ 0`
Two water taps together can fill a tank in `9 3/8`hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`x^2-4sqrt2x+6=0`
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
3x2 + 11x + 10 = 0
`2/x^2-5/x+2=0`
By using the method of completing the square, show that the equation `2x^2+x+4=0` has no real roots.
The sum of the areas of two squares is `640m^2` . If the difference in their perimeter be 64m, find the sides of the two square
Fill in the gap and complete.

Fill in the gaps and complete.
If α, β are roots of quadratic equation,
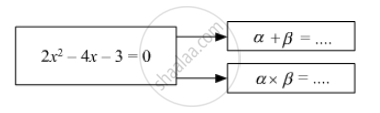
Find the value of discriminant.
2y2 – 5y + 10 = 0
Form the quadratic equation from the roots given below.
3 and –10
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
The difference of two natural numbers is 3 and the difference of their reciprocals is \[\frac{3}{28}\].Find the numbers.
The value of \[\sqrt{6 + \sqrt{6 + \sqrt{6 +}}} . . . .\] is
One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are:
The positive root of `sqrt(3"x"^2 + 6)` = 9 is:
Rohini had scored 10 more marks in her mathematics test out of 30 marks, 9 times these marks would have been the square of her actual marks. How many marks did she get on the test?
If a, b, care in continued proportion, then show that `(a + b)^2/(ab) = (b + c)^2/(bc)`.
Since a, b, c are in continued proportion
∴ `a/b = square/square` = k(say)
⇒ b = `square`, a = `square` = `square`.k = `square`.k2
Now, L.H.S. = `(a + b)^2/(a.square) = (square + square)^2/(square*square)`
= `(squarek^2(k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
R.H.S. = `(b + c)^2/(b.square) = (square + square)^2/(square*square) = (square (k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
L.H.S. = `square`
