Advertisements
Advertisements
Question
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
Solution
α, β are roots of y2 – 2y –7 = 0
\[a = 1, b = - 2, c = - 7\]
\[ = \left( 2 \right)^3 - 3\left( - 7 \right)\left( 2 \right)\]
\[ = 8 + 42\]
\[ = 50\]
APPEARS IN
RELATED QUESTIONS
Find the roots of the quadratic equations `4x^2+4sqrt3x + 3 = 0` by applying the quadratic formula.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`x^2-4sqrt2x+6=0`
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
3x2 + 11x + 10 = 0
`3x^2-2x-1=0`
`5x^2-6x-2=0`
`4x^2+4bx-(a^2-b^2)=0`
`sqrt2x^3-3x-2sqrt2=0`
The sum of the areas of two squares is `640m^2` . If the difference in their perimeter be 64m, find the sides of the two square
The length of a rectangle is thrice as long as the side of a square. The side of the square is 4 cm more than the width of the rectangle. Their areas being equal, find the dimensions.
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares ?
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
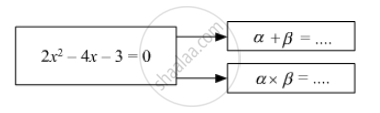
Find the value of discriminant.
`sqrt2x^2 + 4x + 2sqrt2 = 0`
Form the quadratic equation from the roots given below.
\[\frac{1}{2}, - \frac{1}{2}\]
Form the quadratic equation from the roots given below.
\[2 - \sqrt{5}, 2 + \sqrt{5}\]
Sum of the area of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of two squares.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduced by 200 km/hr and the time of the flight increased by 30 minutes. Find the scheduled duration of the flight.
The value of `sqrt(6 + sqrt(6 + sqrt(6 ....)))`
