Advertisements
Advertisements
Question
Choose the correct answer for the following question.
\[\sqrt{5} m^2 - \sqrt{5}m + \sqrt{5} = 0\] which of the following statement is true for this given equation?
Options
Real and uneual roots
Real and equal roots
Roots are not real
Three roots
Solution
For the given quadratic equation \[\sqrt{5} m^2 - \sqrt{5}m + \sqrt{5} = 0\]
\[\text{D} = b^2 - 4ac = \left( - \sqrt{5} \right)^2 - 4 \times \sqrt{5} \times \sqrt{5} = 5 - 20 = - 15\]
Since D < 0 so, the roots are not real.
Hence, the correct answer is Roots are not real.
APPEARS IN
RELATED QUESTIONS
(a) `3x-x^2=x^2+5` (b) `(x+2)^2=2(x^2-5)`
(c) `(sqrt2x+3)^2=2x^2+6` (d)` (x-1)^2=3x^2+x-2`
If α and β are the roots of the equation `3x^2+8x+2=0` then (1/α+1/β)=?
(a)` -3/8` (b) `2/3` `(c) -4 (d)4`
If the equation `4x^2-3kx+1=0` has equal roots then value of k=?
(a)`+-2/3` (b)`+-1/3`
(c)` +-3/4` (d) `+-4/3`
For what value of k, the equation `kx^2-6x2=0` has real roots?
(a) `k≤-9/2` (b)`k≥-9/2`
(c)` k≤-2` (d) None of these
If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0 then ab equals: ?
Decide whether the following equation is quadratic equation or not.
x2 + 5x – 2 = 0
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
x2 + 5x = –(3 – x)
In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of following flow chart.

Which one is the quadratic equation?
Solve the following quadratic equation.
(2x + 3)2 = 25
If 3x + 5y = 9 and 5x + 3y = 7 find the value of x + y.
Obtain a quadratic equation whose roots are –3 and –7.
Two water taps together can fill a tank in `1 7/8` hours. The tap with a longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
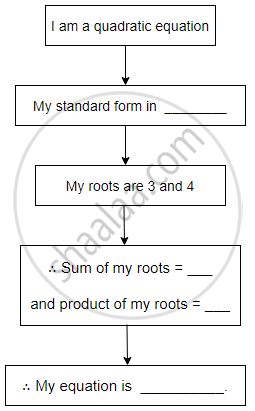
Complete the following activity to form a quadratic equation.
Activity:
Solve for x : `1/(2a + b + 2x) =1/(2a) + 1/b + 1/(2x); x ≠ 0, x ≠ (−2a −b)/2`, a, b ≠ 0
If both the roots of the quadratic equation x2 – 2kx + k2 + k – 5 = 0 are less than 5, then k lies in the interval is ______.
