Advertisements
Advertisements
Question
In the case given below, find the value of x so that POQ is straight line

Solution
POQ is a straight line.
In the given figure,
∵ POQ is a straight line
∴ ∠POL + ∠LOM + ∠MOQ = 180° (Straight line angles)
⇒ x + 20° + 2x - 30° + 3x - 50°= 180°
⇒ 6x + 20° - 80° = 180°
⇒ 6x - 60° = 180°
⇒ 6x = 180° + 60° = 240°
⇒ x = `240^circ/6`
⇒ x = 40°
∴ x = 40°
APPEARS IN
RELATED QUESTIONS
In your note-book copy the following angle using ruler and a pair compass only.
Draw line AB = 6 cm. Construct angle ABC = 60°. Then draw the bisector of angle ABC.
Draw a line segment AB = 6.5 cm. Locate a point P that is 5 cm from A and 4.6 cm from B. Through the point P, draw a perpendicular on to the line segment AB.
Draw a line segment OA = 5 cm. Use set-square to construct angle AOB = 60°, such that OB = 3 cm. Join A and B; then measure the length of AB.
Draw a line segment OP = 8cm. Use set-square to construct ∠POQ = 90°; such that OQ = 6 cm. Join P and Q; then measure the length of PQ.
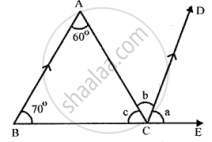
In the following figure, BA is parallel to CD. Find the angles a, b and c:
In the following figures, PQ is parallel to RS. Find the angles a, b and c:
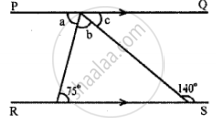
In the following figures, PQ is parallel to RS. Find the angles a, b and c:

Two straight lines are cut by a transversal so that the co-interior angles are supplementary. Are the straight lines parallel?
Draw a line segment AB = 6 cm. Without using set squares, draw angle OAB = 60° and angle OBA = 90°. Measure angle AOB and write this measurement.
