Advertisements
Advertisements
Question
In a triangle OAB,\[\angle\]AOB = 90º. If P and Q are points of trisection of AB, prove that \[{OP}^2 + {OQ}^2 = \frac{5}{9} {AB}^2\]
Solution
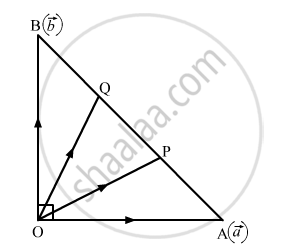
In triangle OAB,\[\angle\]AOB = 90º. P and Q are points of trisection of AB.
Taking O as the origin, let the position vectors of A and B be \[\vec{a}\] and \[\vec{b}\] respectively.
Since P and Q are the points of trisection of AB, so AP : PB = 1 : 2 and AQ : QB = 2 : 1.
Position vector of P, \[\vec{OP} = \frac{2 \vec{a} + \vec{b}}{3}\] ..................(Using section formula)
Position vector of Q,
\[\vec{OQ} = \frac{\vec{a} + 2 \vec{b}}{3}\]
\[\therefore \vec{a} . \vec{b} = 0\] ................(1)
Now,
\[{OP}^2 + {OQ}^2 \]
\[ = \left| \vec{OP} \right|^2 + \left| \vec{OQ} \right|^2 \]
\[ = \left( \frac{2 \vec{a} + \vec{b}}{3} \right) . \left( \frac{2 \vec{a} + \vec{b}}{3} \right) + \left( \frac{\vec{a} + 2 \vec{b}}{3} \right) . \left( \frac{\vec{a} + 2 \vec{b}}{3} \right)\]
\[ = \frac{4 \left| \vec{a} \right|^2 + 4 \vec{a} . \vec{b} + \left| \vec{b} \right|^2 + \left| \vec{a} \right|^2 + 4 \vec{a} . \vec{b} + 4 \left| \vec{b} \right|^2}{9}\]
\[= \frac{5 \left| \vec{a} \right|^2 + 5 \left| \vec{b} \right|^2}{9}.............. \left[ \text{ Using } \left( 1 \right) \right]\]
\[ = \frac{5}{9}\left( \left| \vec{a} \right|^2 + \left| \vec{b} \right|^2 \right)\]
\[ = \frac{5}{9} \left| \vec{AB} \right|^2 ........................\left[ \text{ Using Pythagoras Theorem } \right]\]
\[ = \frac{5}{9} {AB}^2\]
APPEARS IN
RELATED QUESTIONS
Prove that: If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Prove that the diagonals of a rhombus are perpendicular bisectors of each other.
If AD is the median of ∆ABC, using vectors, prove that \[{AB}^2 + {AC}^2 = 2\left( {AD}^2 + {CD}^2 \right)\]
If the median to the base of a triangle is perpendicular to the base, then triangle is isosceles.
Let `A (bara)` and `B (barb)` are any two points in the space and `"R"(bar"r")` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r = (mbarb + nbara)/(m + n) `
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hati - hatj + 3hatk` and `- 5hati + 2hatj - 5hatk` in the ratio 3:2 is internally.
The position vector of points A and B are `6bar"a" + 2bar"b"` and `bar"a" - 3bar"b"`. If the point C divides AB in the ratio 3 : 2, show that the position vector of C is `3bar"a" - bar"b"`.
Prove that the median of a trapezium is parallel to the parallel sides of the trapezium and its length is half of the sum of the lengths of the parallel sides.
Prove that `(bar"a" xx bar"b").(bar"c" xx bar"d")` =
`|bar"a".bar"c" bar"b".bar"c"|`
`|bar"a".bar"d" bar"b".bar"d"|.`
Find the volume of a parallelopiped whose coterimus edges are represented by the vectors `hat"i" + hat"k", hat"i" + hat"k", hat"i" + hat"j"`. Also find volume of tetrahedron having these coterminus edges.
Prove that altitudes of a triangle are concurrent
In a quadrilateral ABCD, M and N are the mid-points of the sides AB and CD respectively. If AD + BC = tMN, then t = ____________.
In a triangle ABC, if `1/(a + c) + 1/(b + c) = 3/(a + b + c)` then angle C is equal to ______
P is the point of intersection of the diagonals of the parallelogram ABCD. If O is any point, then `overline"OA" + overline"OB" + overline"OC" + overline"OD"` = ______
If the position vectors of points A and B are `hati + 8hatj + 4hatk` and `7hati + 2hatj - 8hatk`, then what will be the position vector of the midpoint of AB?
If G and G' are the centroids of the triangles ABC and A'B'C', then `overline("A""A"^') + overline("B""B"^') + overline("C""C"^')` is equal to ______
The image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3` is ______
The co-ordinates of the points which divides line segment joining the point A(2, –6, 8) and B(–1, 3,–4) internally in the ratio 1: 3' are ______.
Let `square`PQRS be a quadrilateral. If M and N are midpoints of the sides PQ and RS respectively then `bar"PS" + bar"OR"` = ______.
In ΔABC, P is the midpoint of BC, Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2, then ______.
Find the unit vector in the diret:tion of the vector `veca = hati + hatj + 2hatk`
If D, E, F are the mid points of the sides BC, CA and AB respectively of a triangle ABC and 'O' is any point, then, `|vec(AD) + vec(BE) + vec(CF)|`, is ______.
In ΔABC the mid-point of the sides AB, BC and CA are respectively (l, 0, 0), (0, m, 0) and (0, 0, n). Then, `("AB"^2 + "BC"^2 + "CA"^2)/("l"^2 + "m"^2 + "n"^2)` is equal to ______.
ΔABC has vertices at A = (2, 3, 5), B = (–1, 3, 2) and C = (λ, 5, µ). If the median through A is equally inclined to the axes, then the values of λ and µ respectively are ______.
If G(g), H(h) and (p) are centroid orthocentre and circumcentre of a triangle and xp + yh + zg = 0, then (x, y, z) is equal to ______.
The position vector of points A and B are `6bara +2barb ` and `bara-3barb `.If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara-barb` .
The position vector of points A and B are `6bara + 2 barb` and `bara-3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara -barb`.
The position vector of points A and B are `6bara + 2barb` and `bara - 3barb`. If the point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6 bara + 2barb and bara - 3barb.` If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara - barb.`
The position vector of points A and B are `6 bara + 2 barb and bara - 3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3 bara - barb`.
The position vector of points A and B are 6`bara + 2barb and bara - 3barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is 3`bara - barb`.
