Advertisements
Advertisements
Question
In which of the following decays the atomic number decreases?
(a) α-decay
(b) β+-decay
(c) β−-decay
(d) γ-decay
Advertisements
Solution
(a) α-decay
(b) β+-decay
In alpha particle decay, the unstable nucleus emits an alpha particle reducing its proton number (atomic number) Z as well as neutron number N by 2.
`""_Z^AX` → `""_(Z-2)^(A-4)Y` + `""_2^4He`
During β−-decay, a neutron is converted to a proton, an electron and an antineutrino. Thus, there is an increase in the atomic number.
`""_Z^AX` → `""_(Z+1)^(A)Y` + `e^-` +`barnu`
During β+-decay, a proton in the nucleus is converted to a neutron, a positron and a neutrino in order to maintain the stability of the nucleus. Thus, there is a decrease in the atomic number.
`""_Z^AX` → `""_(Z-1)^(A)Y` + `β^+` +`nu`
When a nucleus is in higher excited state or has excess of energy, it comes to the lower state in order to become stable and release energy in the form of electromagnetic radiation called gamma ray. The element in the gamma decay doesn't change.
Therefore, alpha and beta plus decay suffer decrease in atomic number.
APPEARS IN
RELATED QUESTIONS
Write symbolically the nuclear β+ decay process of `""_6^11C` Is the decayed product X an isotope or isobar of (`""_6^11C`)? Given the mass values m (`""_6^11C`) = 11.011434 u and m (X) = 11.009305 u. Estimate the Q-value in this process.
Obtain the binding energy of the nuclei `""_26^56"Fe"` and `""_83^209"Bi"` in units of MeV from the following data:
`"m"(""_26^56"Fe")` = 55.934939 u
`"m"(""_83^209"Bi")`= 208.980388 u
What is meant by the terms half-life of a radioactive substance and binding energy of a nucleus?
Define the terms (i) half-life (T1/2) and (ii) average life (τ). Find out their relationships with the decay constant (λ).
Find the binding energy per nucleon of `""_79^197"Au"` if its atomic mass is 196.96 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
What is the minimum energy which a gamma-ray photon must possess in order to produce electron-positron pair?
In a nuclear reactor, what is the function of:
(i) The moderator
(ii) The control rods
(iii) The coolant
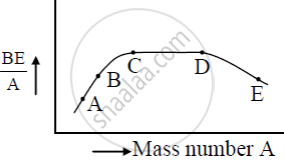
Sketch a graph showing the variation of binding energy per nucleon of a nucleus with its mass number.
The figure shows the plot of binding energy (BE) per nucleon as a function of mass number A. The letters A, B, C, D, and E represent the positions of typical nuclei on the curve. Point out, giving reasons, the two processes (in terms of A, B, C, D, and E ), one of which can occur due to nuclear fission and the other due to nuclear fusion.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are\[\ce{_12^24Mg}\](23.98504 u), \[\ce{_12^25Mg}\] (24.98584 u), and \[\ce{_12^26Mg}\] (25.98259 u). The natural abundance of \[\ce{_12^24Mg}\] is 78.99% by mass. Calculate the abundances of other two isotopes.
A body's centre of mass
He23 and He13 nuclei have the same mass number. Do they have the same binding energy?
The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge e′: F = `1/(4πε_0) e^('2)/r` estimate the value of (e’/e) given that the binding energy of a deuteron is 2.2 MeV.
Find the binding energy of a H-atom in the state n = 2
Explain the release of energy in nuclear fission and fusion on the basis of binding energy per nucleon curve.
State the significance of binding energy per nucleon.
What is meant by “binding energy per nucleon” of a nucleus?
