Advertisements
Advertisements
Question
Derive an expression for the total energy of electron in ‘n' th Bohr orbit. Hence show that energy of the electron is inversely proportional to the square of principal quantum number. Also define binding energy.
Solution
Expression for total energy of electron in the nth orbit (En)
i. Kinetic energy (K.E.):
Let, m = mass of electron
rn = radius of nth orbit of Bohr’s hydrogen atom
vn = velocity of electron
−e = charge of electron
+e = charge on the nucleus
According to Bohr’s first postulate,
`(mv_n^2)/r_n=1/(4piin_0)xxe^2/r_n^2`
where, ε0 is permittivity of free space.
`(mv_n^2)=1/(4piin_0)xxe^2/r_n` ................(1)
The revolving electron in the circular orbit has linear speed and hence it possesses kinetic energy.
It is given by,
K.E=`1/2mv_n^2`
∴K.E =`1/2 1/(4piin_0)xxe^2/r_n` from equation (1)
∴K.E=`e^2/(8piin_0r_n)` ............................(2)
ii. Potential energy (P.E.):
Potential energy of electron is given by, P.E = V(−e)
where, V = electric potential at any point due to charge on nucleus
− e = charge on electron.
P.E=`1/(4piin_0)e/r_nxx(-e)`
P.E=`1/(4piin_0) xx -e^2/r_n`
P.E=`-e^2/(4piin_0r_n)` ........................ (3)
iii. Total energy (En):
The total energy of the electron in any orbit is its sum of P.E and K.E.
∴ T.E = K.E + P.E
=`e^2/(8piin_0r_n) + -e^2/(4piin_0r_n) ` [From equations (ii) and (iii)]
`E_n=-1/(8piin_0) e^2/r_n`
`E_n=-e^2/(8piin_0r_n) ` .................(4)
iv. But, `r_n=((in_0h^2)/(pime^2))n^2`
Substituting for rn in equation (iv),
`E_n=-1/(8piin_0) e^2/(((in_0h^2)/(pime^2))n^2) `
`=-1/(8piin_0) (e^2pime^2)/(in_0h^2n^2)`
`=-((me^4)/(8in_0^2h^2))1/n^2` ..........(5)
This is required expression for energy of electron in nth orbit of Bohr’s hydrogen atom
v. The negative sign in equation (v) shows that the electron is bound to the nucleus by an attractive force and hence energy must be supplied to the electron in order to make it free from the influence of the nucleus.
vi. Now, as m, e, ε0, and h in equation (v) are constant,
`(me^4)/(8in_0^2h^2)=constant`
Using equation (v), we get,
`E_n="constant"(1/n^2)`
`E_n prop 1/n^2`
Hence, the total energy of electron in a Bohr’s orbit is inversely proportional to the square of the principal quantum number.
The amount of energy required to separate all the nucleons from the nucleus is called binding energy of the nucleus.
APPEARS IN
RELATED QUESTIONS
Is the nucleus formed in the decay of the nucleus `""_11^22Na`, an isotope or isobar?
Obtain the binding energy (in MeV) of a nitrogen nucleus `(""_7^14"N")`, given `"m"(""_7^14"N")` = 14.00307 u.
Obtain the binding energy of the nuclei `""_26^56"Fe"` and `""_83^209"Bi"` in units of MeV from the following data:
`"m"(""_26^56"Fe")` = 55.934939 u
`"m"(""_83^209"Bi")`= 208.980388 u
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei `""_20^41"Ca"` and `""_13^27 "Al"` from the following data:
`"m"(""_20^40"Ca")` = 39.962591 u
`"m"(""_20^41"Ca")` = 40.962278 u
`"m"(""_13^26"Al")` = 25.986895 u
`"m"(""_13^27"Al")` = 26.981541 u
Consider the fission of `""_92^238"U"` by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are `""_58^140"Ce"` and `""_44^99"Ru"`. Calculate Q for this fission process. The relevant atomic and particle masses are
`"m"(""_92^238"U")` = 238.05079 u
`"m"(""_58^140"Ce")` = 139.90543 u
`"m"(""_44^99"Ru")` = 98.90594 u
What is meant by the terms half-life of a radioactive substance and binding energy of a nucleus?
Define half-life of a radioactive substance
Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number ‘A’ lying 30 < A < 170?
Is it easier to take out a nucleon (a) from carbon or from iron (b) from iron or from lead?
In which of the following decays the atomic number decreases?
(a) α-decay
(b) β+-decay
(c) β−-decay
(d) γ-decay
How much energy is released in the following reaction : 7Li + p → α + α.
Atomic mass of 7Li = 7.0160 u and that of 4He = 4.0026 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
What is the minimum energy which a gamma-ray photon must possess in order to produce electron-positron pair?
Calculate mass defect and binding energy per nucleon of `"_10^20 Ne`, given
Mass of `"_10^20 Ne= 19.992397` u
Mass of `"_0^1H = 1.007825` u
Mass of `"_0^1n = 1.008665` u
Sketch a graph showing the variation of binding energy per nucleon of a nucleus with its mass number.
The figure shows the plot of binding energy (BE) per nucleon as a function of mass number A. The letters A, B, C, D, and E represent the positions of typical nuclei on the curve. Point out, giving reasons, the two processes (in terms of A, B, C, D, and E ), one of which can occur due to nuclear fission and the other due to nuclear fusion.
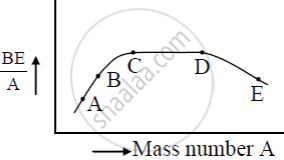
Answer the following question.
Draw the curve showing the variation of binding energy per nucleon with the mass number of nuclei. Using it explains the fusion of nuclei lying on the ascending part and fission of nuclei lying on the descending part of this curve.
Calculate the binding energy of an alpha particle given its mass to be 4.00151 u.
An electron in hydrogen atom stays in its second orbit for 10−8 s. How many revolutions will it make around the nucleus at that time?
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are\[\ce{_12^24Mg}\](23.98504 u), \[\ce{_12^25Mg}\] (24.98584 u), and \[\ce{_12^26Mg}\] (25.98259 u). The natural abundance of \[\ce{_12^24Mg}\] is 78.99% by mass. Calculate the abundances of other two isotopes.
Determine the binding energy per nucleon of the americium isotope \[\ce{_95^244Am}\], given the mass of \[\ce{_95^244Am}\] to be 244.06428 u.
The difference in mass of a nucleus and its constituents is called ______.
A body's centre of mass
Mx and My denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a β– decay is Q1 and that for a β+ decay is Q2. If m e denotes the mass of an electron, then which of the following statements is correct?
Heavy stable nucle have more neutrons than protons. This is because of the fact that ______.
The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge e′: F = `1/(4πε_0) e^('2)/r` estimate the value of (e’/e) given that the binding energy of a deuteron is 2.2 MeV.
Nuclei with magic no. of proton Z = 2, 8, 20, 28, 50, 52 and magic no. of neutrons N = 2, 8, 20, 28, 50, 82 and 126 are found to be very stable.
(i) Verify this by calculating the proton separation energy Sp for 120Sn (Z = 50) and 121Sb = (Z = 51).
The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by `S_P = (M_(z-1^' N) + M_H - M_(ZN))c^2`.
Given 119In = 118.9058u, 120Sn = 119.902199u, 121Sb = 120.903824u, 1H = 1.0078252u.
(ii) What does the existance of magic number indicate?
Find the binding energy of a H-atom in the state n = 2
Define binding energy per nucleon.
State the significance of binding energy per nucleon.
Calculate the values of x and y in the following nuclear reaction.
\[\ce{^227_89Ac -> ^211_82Pb + x[^4_2He]+ y[^0_-1e]}\]
What is binding energy of nucleus?
What is meant by “binding energy per nucleon” of a nucleus?
Find the binding energy per nucleon of 235U based on the information given below.
| Mass(u) | |
| mass of neutral `""_92^235"U"` | 235.0439 |
| mass of a proton | 1.0073 |
| mass of a neutron | 1.0087 |
