Advertisements
Advertisements
प्रश्न
Derive an expression for the total energy of electron in ‘n' th Bohr orbit. Hence show that energy of the electron is inversely proportional to the square of principal quantum number. Also define binding energy.
उत्तर
Expression for total energy of electron in the nth orbit (En)
i. Kinetic energy (K.E.):
Let, m = mass of electron
rn = radius of nth orbit of Bohr’s hydrogen atom
vn = velocity of electron
−e = charge of electron
+e = charge on the nucleus
According to Bohr’s first postulate,
`(mv_n^2)/r_n=1/(4piin_0)xxe^2/r_n^2`
where, ε0 is permittivity of free space.
`(mv_n^2)=1/(4piin_0)xxe^2/r_n` ................(1)
The revolving electron in the circular orbit has linear speed and hence it possesses kinetic energy.
It is given by,
K.E=`1/2mv_n^2`
∴K.E =`1/2 1/(4piin_0)xxe^2/r_n` from equation (1)
∴K.E=`e^2/(8piin_0r_n)` ............................(2)
ii. Potential energy (P.E.):
Potential energy of electron is given by, P.E = V(−e)
where, V = electric potential at any point due to charge on nucleus
− e = charge on electron.
P.E=`1/(4piin_0)e/r_nxx(-e)`
P.E=`1/(4piin_0) xx -e^2/r_n`
P.E=`-e^2/(4piin_0r_n)` ........................ (3)
iii. Total energy (En):
The total energy of the electron in any orbit is its sum of P.E and K.E.
∴ T.E = K.E + P.E
=`e^2/(8piin_0r_n) + -e^2/(4piin_0r_n) ` [From equations (ii) and (iii)]
`E_n=-1/(8piin_0) e^2/r_n`
`E_n=-e^2/(8piin_0r_n) ` .................(4)
iv. But, `r_n=((in_0h^2)/(pime^2))n^2`
Substituting for rn in equation (iv),
`E_n=-1/(8piin_0) e^2/(((in_0h^2)/(pime^2))n^2) `
`=-1/(8piin_0) (e^2pime^2)/(in_0h^2n^2)`
`=-((me^4)/(8in_0^2h^2))1/n^2` ..........(5)
This is required expression for energy of electron in nth orbit of Bohr’s hydrogen atom
v. The negative sign in equation (v) shows that the electron is bound to the nucleus by an attractive force and hence energy must be supplied to the electron in order to make it free from the influence of the nucleus.
vi. Now, as m, e, ε0, and h in equation (v) are constant,
`(me^4)/(8in_0^2h^2)=constant`
Using equation (v), we get,
`E_n="constant"(1/n^2)`
`E_n prop 1/n^2`
Hence, the total energy of electron in a Bohr’s orbit is inversely proportional to the square of the principal quantum number.
The amount of energy required to separate all the nucleons from the nucleus is called binding energy of the nucleus.
APPEARS IN
संबंधित प्रश्न
Is the nucleus formed in the decay of the nucleus `""_11^22Na`, an isotope or isobar?
Obtain the binding energy (in MeV) of a nitrogen nucleus `(""_7^14"N")`, given `"m"(""_7^14"N")` = 14.00307 u.
Obtain the binding energy of the nuclei `""_26^56"Fe"` and `""_83^209"Bi"` in units of MeV from the following data:
`"m"(""_26^56"Fe")` = 55.934939 u
`"m"(""_83^209"Bi")`= 208.980388 u
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei `""_20^41"Ca"` and `""_13^27 "Al"` from the following data:
`"m"(""_20^40"Ca")` = 39.962591 u
`"m"(""_20^41"Ca")` = 40.962278 u
`"m"(""_13^26"Al")` = 25.986895 u
`"m"(""_13^27"Al")` = 26.981541 u
What is meant by the terms half-life of a radioactive substance and binding energy of a nucleus?
What is the significance of binding energy per nucleon of a nucleus of a radioactive element?
Define half-life of a radioactive substance
Define the terms (i) half-life (T1/2) and (ii) average life (τ). Find out their relationships with the decay constant (λ).
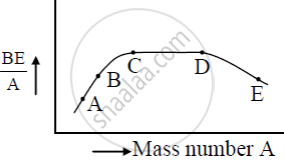
Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number ‘A’ lying 30 < A < 170?
Is it easier to take out a nucleon (a) from carbon or from iron (b) from iron or from lead?
If the nucleons of a nucleus are separated from each other, the total mass is increased. Where does this mass come from?
In which of the following decays the atomic number decreases?
(a) α-decay
(b) β+-decay
(c) β−-decay
(d) γ-decay
How much energy is released in the following reaction : 7Li + p → α + α.
Atomic mass of 7Li = 7.0160 u and that of 4He = 4.0026 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Find the binding energy per nucleon of `""_79^197"Au"` if its atomic mass is 196.96 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Which property of nuclear force explains the constancy of binding energy per nucleon `((BE)/A)` for nuclei in the range 20< A < 170 ?
What is the minimum energy which a gamma-ray photon must possess in order to produce electron-positron pair?
Binding energy per nucleon for helium nucleus (2 He) is 7.0 MeV Find value of mass defect for helium nucleus
In a nuclear reactor, what is the function of:
(i) The moderator
(ii) The control rods
(iii) The coolant
The figure shows the plot of binding energy (BE) per nucleon as a function of mass number A. The letters A, B, C, D, and E represent the positions of typical nuclei on the curve. Point out, giving reasons, the two processes (in terms of A, B, C, D, and E ), one of which can occur due to nuclear fission and the other due to nuclear fusion.
Calculate the binding energy of an alpha particle given its mass to be 4.00151 u.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are\[\ce{_12^24Mg}\](23.98504 u), \[\ce{_12^25Mg}\] (24.98584 u), and \[\ce{_12^26Mg}\] (25.98259 u). The natural abundance of \[\ce{_12^24Mg}\] is 78.99% by mass. Calculate the abundances of other two isotopes.
Determine the binding energy per nucleon of the americium isotope \[\ce{_95^244Am}\], given the mass of \[\ce{_95^244Am}\] to be 244.06428 u.
The difference in mass of a nucleus and its constituents is called ______.
A body's centre of mass
Mx and My denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a β– decay is Q1 and that for a β+ decay is Q2. If m e denotes the mass of an electron, then which of the following statements is correct?
Heavy stable nucle have more neutrons than protons. This is because of the fact that ______.
He23 and He13 nuclei have the same mass number. Do they have the same binding energy?
The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge e′: F = `1/(4πε_0) e^('2)/r` estimate the value of (e’/e) given that the binding energy of a deuteron is 2.2 MeV.
Find the binding energy of a H-atom in the state n = 2
Calculate the binding energy of an alpha particle in MeV. Given
mass of a proton = 1.007825 u
mass of a neutron = 1.008665 u
mass of He nucleus = 4.002800 u
1u = 931 MeV/c2
Define binding energy per nucleon.
State the significance of binding energy per nucleon.
Which of the following quantities is a measure of stability of nucleus?
Calculate the values of x and y in the following nuclear reaction.
\[\ce{^227_89Ac -> ^211_82Pb + x[^4_2He]+ y[^0_-1e]}\]
What is binding energy of nucleus?
What is meant by “binding energy per nucleon” of a nucleus?
Find the binding energy per nucleon of 235U based on the information given below.
| Mass(u) | |
| mass of neutral `""_92^235"U"` | 235.0439 |
| mass of a proton | 1.0073 |
| mass of a neutron | 1.0087 |
