Advertisements
Advertisements
Question
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
Solution
Let a be the side of square.
We are given that the circle is inscribed in the square.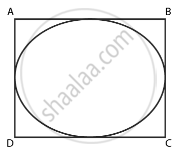
Diameter of circle = Side of square = a
Radius of the circle = `"a"/2`
Area of the circle = πr2
= `π("a"/2)^2`
= `(π"a"^2)/4` cm2
Hence, area of the circle is `(π"a"^2)/4` cm2
Thus the area of the circle inscribed in a square of side a cm is not a2 cm2
APPEARS IN
RELATED QUESTIONS
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
The diameter of a wheel is 40 cm. How many revolutions will it make in covering 176 m?
The area of the sector of angle θ° of a circle with radius R is
The formula used to find the area of the circle is ________ sq.units
