Advertisements
Advertisements
Question
किसी AP के प्रथम पाँच पदों के योग और उसी AP के प्रथम सात पदों के योग का योग 167 है। यदि इस AP के प्रथम दस पदों का योग 235 है, तो इसके प्रथम 20 पदों का योग ज्ञात कीजिए।
Solution
मान लीजिए कि एक AP का पहला पद, सार्व अंतर और पदों की संख्या क्रमशः a, d और n हैं।
∵ AP के प्रथम n पदों का योग,
Sn = `n/2[2a + (n - 1)d]` ...(i)
∴ किसी AP के पहले पाँच पदों का योग,
S5 = `5/2[2a + (5 - 1)d]` ...[समीकरण (i) से]
= `5/2(2a + 4d)`
= 5(a + 2d)
⇒ S5 = 5a + 10d ...(ii)
और किसी AP के पहले सात पदों का योग,
S7 = `7/2[2a + (7 - 1)d]`
= `7/2[2a + 6d]`
= 7(a + 3d)
⇒ S7 = 7a + 21d ...(iii)
अब, दी गई शर्त से,
S5 + S7 = 167
⇒ 5a + 10d + 7a + 21d = 167
⇒ 12a + 31d = 167 ...(iv)
दिया गया है कि, इस AP के पहले दस पदों का योग 235 है।
∴ S10 = 235
⇒ `10/2 [2a + (10 - 1)d]` = 235
⇒ 5(2a + 9d) = 235
⇒ 2a + 9d = 47 ...(v)
समीकरण (v) को 6 से गुणा करके समीकरण (iv) में घटाने पर, हमें प्राप्त होता है।
12a + 54d = 282
12a + 31d = 167
– – –
23d = 115
⇒ d = 5
अब, d का मान समीकरण (v) में रखें, हमें मिलता है।
2a + 9(5) = 47
⇒ 2a + 45 = 47
⇒ 2a = 47 – 45 = 2
⇒ a = 1
इस AP के पहले बीस पदों का योग,
S20 = `20/2[2a + (20 - 1)d]`
= 10[2 × (1) + 19 × (5)]
= 10(2 + 95)
= 10 × 97
= 970
अतः, इसके पहले बीस पदों का आवश्यक योग 970 है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
`1/15,1/12,1/10`, ...., 11 पदों तक
नीचे दिए गए योगफल को ज्ञात कीजिए:
34 + 32 + 30 + ... + 10
एक A.P. में, a = 7 और a13 = 35 दिया है। d और S13 ज्ञात कीजिए।
एक A.P. में, a = 8, an = 62 और Sn = 210 दिया है। n और d ज्ञात कीजिए।
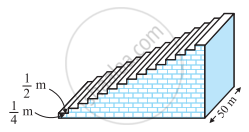
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट (concrete) की बनी है। प्रत्येक सीढ़ी में `1/4` m की चढ़ाई है और `1/2` m का फैलाव (चौड़ाई) है। (देखिए आकृति)।इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = `1/4 xx 1/2 xx 50` m3 है।]
यदि किसी AP का प्रथम पद –5 और सार्व अंतर 2 है, तो उसके प्रथम 6 पदों का योग ______ है।
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
प्रथम पद 8 और सार्व अंतर 20 वाली एक AP के प्रथम n पदों का योग एक अन्य AP के प्रथम 2n पदों के योग के बराबर है, जिसका प्रथम पद –30 और सार्व अंतर 8 है। n ज्ञात कीजिए।
ज्ञात कीजिए :
1 और 500 के बीच के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
समीकरण – 4 + (−1) + 2 + ... + x = 437 को हल कीजिए।
