Advertisements
Advertisements
Question
प्रथम पद 8 और सार्व अंतर 20 वाली एक AP के प्रथम n पदों का योग एक अन्य AP के प्रथम 2n पदों के योग के बराबर है, जिसका प्रथम पद –30 और सार्व अंतर 8 है। n ज्ञात कीजिए।
Solution
दिया गया है, पहले AP(a) का पहला पद = 8
और पहले AP(d) का सार्व अंतर = 20
माना पहले AP में पदों की संख्या n है।
∵ AP के प्रथम n पदों का योग,
Sn = `n/2 [2a + (n - 1)d]`
∴ Sn = `n/2[2 xx 8 + (n - 1)20]`
⇒ Sn = `n/2(16 + 20n - 20)`
⇒ Sn = `n/2(20n - 4)`
∴ Sn = n(10n – 2) ...(i)
अब, दूसरे AP(a') का पहला पद = – 30
और दूसरे AP(d') का सार्व अंतर = 8
∴ दूसरे AP के पहले 2n पदों का योग,
S2n = `(2n)/2 [2a + (2n - 1)d]`
⇒ S2n = n[2(– 30) + (2n – 1)(8)]
⇒ S2n = n[– 60 + 16n – 8)]
⇒ S2n = n[16n – 68] ...(ii)
अब, दी गई शर्त से,
पहले AP के पहले n पदों का योग = दूसरे AP के प्रथम 2n पदों का योग
⇒ Sn = S2n ...[समीकरण (i) और (ii) से]
⇒ n(10n – 2) = n(16n – 68)
⇒ n[(16n – 68) – (10n – 2)] = 0
⇒ n(16n – 68 – 10n + 2) = 0
⇒ n(6n – 66) = 0
⇒ n = 11 ...[∵ n ≠ 0]
अतः, n का अभीष्ट मान 11 है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
-37, -33, -29,....,12 पदों तक
एक A.P. में, a = 2, d = 8 और Sn = 90 दिया है। n और an ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
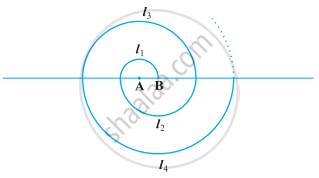
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
3 के प्रथम पाँच गुणजों का योग ______ है।
AP: `- 4/3, -1, -2/3,..., 4 1/3` के दोनों मध्य पदों का योग ज्ञात कीजिए।
AP: –2, –7, –12,... का कौन-सा पद –77 है? पद –77 तक इस AP का योग ज्ञात कीजिए।
ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो 2 का गुणज हैं और 9 का भी गुणज हैं।
[संकेत : 2 और 9 का LCM ज्ञात कीजिए।]
AP: −15, −13, −11,... का योग −55 बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।
यासमीन पहले महीने में 32 रु की बचत करती है, दूसरे महीने में 36 रु की बचत करती है तथा तीसरे महीने में 40 रु की बचत करती है। यदि वह इसी प्रकार बचत करती रहे, तो कितने महीने में वह 2000 रु की बचत कर लेगी?
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
