Advertisements
Advertisements
Question
किसी बारंबारता बंटन में पाँच सतत वर्गों में से प्रत्येक की चौड़ाई 5 है तथा सबसे छोटे वर्ग की निम्न सीमा 10 है। सबसे बड़े वर्ग की उपरि सीमा है :
Options
15
25
35
40
Solution 1
35
स्पष्टीकरण -
मान लीजिए कि x और y बारंबारता बंटन की ऊपरी और निचली वर्ग सीमाएँ हैं।
दिया गया है, वर्ग की चौड़ाई = 5
⇒ x – y = 5 ...(i)
साथ ही, निम्न वर्ग (y) = 10 दिया गया है।
समीकरण (i) में y = 10 रखने पर हम पाते हैं।
x – 10 = 5
⇒ x = 15
इसलिए, निम्न वर्ग की उच्च वर्ग सीमा 15 है।
अतः, उच्चतम वर्ग की ऊपरी वर्ग सीमा
= (निरंतर वर्गों की संख्या × वर्ग चौड़ाई + निम्नतम वर्ग की निम्न वर्ग सीमा)
= 5 × 5 + 10
= 25 + 10
= 35
अतः, उच्चतम वर्ग की ऊपरी वर्ग सीमा 35 है।
Solution 2
35
स्पष्टीकरण -
निम्न वर्ग की उच्च वर्ग सीमा ज्ञात करने के बाद, चौड़ाई 5 के बारंबारता बंटन में पांच सतत वर्ग 10 – 15, 15 – 20, 20 – 25, 25 – 30 और 30 – 35 हैं।
इस प्रकार, उच्चतम वर्ग 30 – 35 है,
अतः, इस वर्ग की ऊपरी सीमा 35 है।
APPEARS IN
RELATED QUESTIONS
मान लीजिए कि एक सतत बारंबारता बंटन में एक वर्ग का मध्य-बिंदु m है और उपरि वर्ग सीमा l है। इस वर्ग की निम्न वर्ग सीमा है :
वर्ग अंतराल 10 – 20, 20 – 30, में संख्या 20 निम्नलिखित में सम्मिलित है :
निम्नलिखित आँकड़ों के लिए, एक अंतराल 250 – 270 (270 सम्मिलित नहीं) लेते हुए बराबर मापों के वर्ग अंतरालों वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है :
268, 220, 368, 258, 242, 310, 272, 342, 310, 290, 300, 320, 319, 304, 402, 318, 406, 292, 354, 278, 210, 240, 330, 316, 406, 215, 258, 236.
वर्ग अंतराल 310 – 330 की बारंबारता है :
निम्नलिखित आँकड़ों के लिए एक वर्ग 63 – 72 (72 सम्मिलित है) लेते हुए बराबर मापों के वर्ग वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है :
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66, 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44.
इस बंटन में वर्गों की संख्या होगी :
यदि n प्रेक्षण x1, x2, ..., xn के माध्य को `barx` से निरूपित किया जाता है, तो `sum_(i = 1)^n (x_i - barx)` का मान है :
बारंबारता सारणी को आलेखीय रूप से नीचे दर्शाए अनुसार निरूपित किया गया है :
| प्राप्तांक | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 100 |
| विद्यार्थियों की संख्या | 10 | 15 | 20 | 25 |
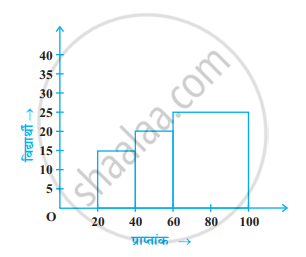
क्या आप सोचते हैं कि यह निरूपण सही है? क्यों?
एक बच्चा कहता है कि 3, 14, 18, 20, 5 का माध्यक 18 है। यह बच्चा माध्यक ज्ञात करने के बारे में क्या नहीं जानता है?
30 बच्चों से पूछा गया कि उन्होंने पिछले सप्ताह कितने घंटे टी.वी. के प्रोग्राम देखे। इसके परिणाम निम्नलिखित रूप में रिकार्ड किए गए :
| घंटों की संख्या | 0 – 5 | 5 – 10 | 10 – 15 | 15 – 20 |
| बारंबारता | 8 | 16 | 4 | 2 |
क्या हम कह सकते हैं कि उस सप्ताह में 10 या उससे अधिक घंटों तक टी वी देखने वाले बच्चों की संख्या 22 है? अपने उत्तर का औचित्य दीजिए।
दिए हुए बारंबारता बंटन को एक सतत वर्गीकृत बंटन में बदलिए :
| वर्ग-अंतराल | बारंबारता |
| 150 – 153 | 7 |
| 154 – 157 | 7 |
| 158 – 161 | 15 |
| 162 – 165 | 10 |
| 166 – 169 | 5 |
| 170 – 173 | 6 |
किन अंतरालों में 153.5 और 157.5 सम्मिलित किए जाएंगे?
किसी महीने में एक परिवार द्वारा विभिन्न मदों पर किए गए व्यय निम्नलिखित हैं :
| मद | भोजन | शिक्षा | कपड़े | मकान किराया | अन्य | बचत |
| व्यय (रु में) | 4000 | 2500 | 1000 | 3500 | 2500 | 1500 |
उपरोक्त को निरूपित करने के लिए एक दंड आलेख खींचिए।
