Advertisements
Advertisements
Question
किसी ऊर्ध्वाधर मीनार की चोटी का भूमि पर स्थित किसी बिंदु से उन्नयन कोण 60° है। पहले बिंदु से 10 m उर्ध्वाधरत: ऊपर एक अन्य बिंदु पर उसका उन्नयन कोण 45° है। मीनार की उँचाई ज्ञात कीजिए।
Solution
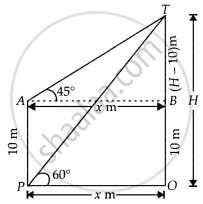
माना ऊर्ध्वाधर मीनार की ऊँचाई है,
OT = H m और OP = AB = x m
दिया गया है, AP = 10 m
और ∠TPO = 60°, ∠TAB = 45°
अब, ∆TPO में,
tan 60° = `"OT"/"OP" = "H"/x`
⇒ `sqrt(3) = "H"/x`
⇒ `x = "H"/sqrt(3)` ...(i)
और ∆TAB में,
tan 45° = `"TB"/"AB" = ("H" - 10)/x`
⇒ 1 = `("H" - 10)/x`
⇒ `x = "H" - 10`
⇒ `"H"/sqrt(3) = "H" - 10` ...[समीकरण (i) से]
⇒ `"H" - "H"/sqrt(3)` = 10
⇒ `"H"(1 - 1/sqrt(3))` = 10
⇒ `"H"((sqrt(3) - 1)/sqrt(3))` = 10
⇒ H = `(10sqrt(3))/(sqrt(3) - 1)`
∴ H = `(10sqrt(3))/(sqrt(3) - 1) * (sqrt(3) + 1)/(sqrt(3) + 1)` ...[युक्तिकरण द्वारा]
= `(10sqrt(3)(sqrt(3) + 1))/(3 - 1)`
= `(10sqrt(3)(sqrt(3) + 1))/2`
⇒ H = `5sqrt(3)(sqrt(3) + 1) = 5(sqrt(3) + 3) "m"`
अतः, मीनार की आवश्यक ऊंचाई `5(sqrt(3) + 3) "m"` है।
APPEARS IN
RELATED QUESTIONS
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बिच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
एक नहर के एक तट पर एक टीवी टॉवर ऊध्वार्रधरत: खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का अन्नयन कोण 30° है। (आकृति देखिए) टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बिच की दूरी ज्ञात कीजिए।
मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
किसी मीनार की चोटी का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दुगुनी हो जाए, तो इसकी चोटी का उन्नयन कोण भी दुगुना हो जाएगा।
किसी बिंदु से एक मीनार की चोटी का उन्नयन कोण 30° है। यदि प्रेक्षक दीवार की ओर 20 मीटर चलता है, तो उन्नयन कोण में 15° की वृद्धि हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
