Advertisements
Advertisements
Question
किसी मीनार की चोटी का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दुगुनी हो जाए, तो इसकी चोटी का उन्नयन कोण भी दुगुना हो जाएगा।
Options
सत्य
असत्य
Solution
यह कथन असत्य है।
स्पष्टीकरण:
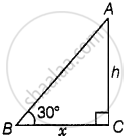
स्थिति I: माना टावर की ऊंचाई h है और BC = x m है।
ΔABC में,
tan 30° = `"AC"/"BC" = "h"/x`
⇒ `1/sqrt(3) = "h"/x` ...(i)
स्थिति II: शर्त के अनुसार, टावर की ऊंचाई दोगुनी है यानी, PR = 2h।
ΔPQR में,
tan θ = `"PR"/"QR" = (2"h")/x`
⇒ tan θ = `2/x xx x/sqrt(3)` ...`[∵ "h" = x/sqrt(3), "समीकरण (i) से"]`
⇒ tan θ = `2/sqrt(3)` = 1.15
∴ θ = tan–1(1.15) < 60°
अत:, अभीष्ट कोण दोगुना नहीं हुआ है।
APPEARS IN
RELATED QUESTIONS
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
भूमि के एक बिंदु से एक 20 मीटर ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमश: 45° और 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बिच की दूरी ज्ञात कीजिए।
एक 1.2 मीटर लंबी लड़की जमीन से 88.2 मीटर की ऊंचाई पर एक क्षैतिज रेखा में हवा के साथ चलते हुए एक गुब्बारे को देखती है। किसी भी क्षण लड़की की आँखों से गुब्बारे का उन्नयन कोण 60° होता है। कुछ समय बाद, उन्नयन कोण घटकर 30° हो जाता है। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
15 मीटर लंबी एक सीढ़ी एक ऊर्ध्वाधर दीवार के ठीक ऊपरी सिरे पर पहुँच पाती है। यदि सीढ़ी इस समय दीवार से 60° का कोण बनाती है, तो दीवार की ऊँचाई ज्ञात कीजिए।
1.5 मीटर ऊँचाई वाला एक प्रेक्षक 22 मीटर ऊँची एक मीनार से 20.5 मीटर की दूरी पर खड़ा है। प्रेक्षक की आँख से मीनार की चोटी का उन्नयन कोण निर्धारित कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
एक समतल भूमि पर खड़ी मीनार की छाया की उस समय की लंबाई जब सूर्य का उन्नयन कोण 30° है, उस समय की लंबाई से 50 m अधिक है जब सूर्य का उन्नयन कोण 60° था। मीनार की ऊँचाई ज्ञात कीजिए।
एक ऊर्ध्वाधर मीनार एक क्षैतिज समतल पर खड़ी है तथा उस पर h ऊँचाई का एक ऊर्ध्वाधर ध्वज-दंड लगा हुआ है। समतल के किसी बिंदु से ध्वज-दंड के निचले और ऊपरी सिरों के उन्नयन कोण क्रमश : α और β हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `((h tan alpha)/(tan beta - tan alpha))` है।
