Advertisements
Advertisements
Question
एक समतल भूमि पर खड़ी मीनार की छाया की उस समय की लंबाई जब सूर्य का उन्नयन कोण 30° है, उस समय की लंबाई से 50 m अधिक है जब सूर्य का उन्नयन कोण 60° था। मीनार की ऊँचाई ज्ञात कीजिए।
Solution
मान लीजिए कि SQ = h मीनार है।
∠SPQ = 30° और ∠SRQ = 60°
प्रश्न के अनुसार,
छाया की लंबाई 50 मीटर लंबी है, सूर्य का उन्नयन कोण 60 डिग्री की तुलना में 30 डिग्री है।
तो, PR = 50 m और RQ = x m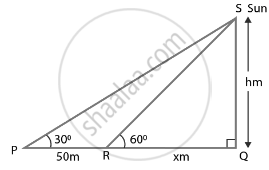
तो ∆SRQ में, हमारे पास है।
tan 60° = `"h"/x` ...`[∵ tan θ = "लंबवत"/"आधार" ⇒ tan 60^circ = "SQ"/"RQ"]`
⇒ `sqrt(3) = "h"/x` ...`[∵ tan 60^circ = sqrt(3)]`
⇒ ` x = "h"/sqrt(3)`
ΔSPQ में,
tan 30° = `"h"/(50 + x)` ...`[∵ tan 30^circ = "SQ"/"PQ" = "SQ"/("PR" + "PQ")]`
⇒ `1/sqrt(3) = "h"/(50 + x)` ...`[∵ tan 30^circ = 1/sqrt(3)]`
⇒ `50 + x = sqrt(3)"h"`
उपरोक्त समीकरण में x का मान प्रतिस्थापित करने पर, हमें प्राप्त होता है।
⇒ `50 + "h"/sqrt(3) = sqrt(3)"h"`
⇒ `(50sqrt(3) + "h")/sqrt(3) = sqrt(3)"h"`
⇒ `50sqrt(3) + "h" = 3"h"`
⇒ `50sqrt(3) = 3"h" - "h"`
⇒ `3"h" - "h" = 50sqrt(3)`
⇒ 2h = `50sqrt(3)`
⇒ h = `(50sqrt(3))/2`
⇒ h = `25sqrt(3)`
अतः, आवश्यक ऊंचाई `25sqrt(3) "m"` है।
APPEARS IN
RELATED QUESTIONS
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बिच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
एक नहर के एक तट पर एक टीवी टॉवर ऊध्वार्रधरत: खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का अन्नयन कोण 30° है। (आकृति देखिए) टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
1.5 मीटर ऊँचाई वाला एक प्रेक्षक 22 मीटर ऊँची एक मीनार से 20.5 मीटर की दूरी पर खड़ा है। प्रेक्षक की आँख से मीनार की चोटी का उन्नयन कोण निर्धारित कीजिए।
किसी बिंदु से एक मीनार की चोटी का उन्नयन कोण 30° है। यदि प्रेक्षक दीवार की ओर 20 मीटर चलता है, तो उन्नयन कोण में 15° की वृद्धि हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए।
किसी ऊर्ध्वाधर मीनार की चोटी का भूमि पर स्थित किसी बिंदु से उन्नयन कोण 60° है। पहले बिंदु से 10 m उर्ध्वाधरत: ऊपर एक अन्य बिंदु पर उसका उन्नयन कोण 45° है। मीनार की उँचाई ज्ञात कीजिए।
किसी मकान की खिड़की भूमि से h m की ऊँचाई पर है। इस खिड़की से, सड़क के दूसरी ओर स्थित एक अन्य मकान के शिखर और आधार के क्रमशः उन्नयन और अवनमन कोण α और β पाए जाते हैं। सिद्ध कीजिए कि दूसरे मकान की ऊँचाई h(1 + tan α cot β) मीटर है।
किसी मकान की निचली खिड़की भूमि से 2 m की ऊँचाई पर है तथा उसकी ऊपरी खिड़की निचली खिड़की से ऊर्ध्वाधरत : 4 m ऊपर है। किसी क्षण इन खिड़कियों से एक गुब्बारे के उन्नयन कोण क्रमश : 60° और 30° प्रेक्षित किए गए। भूमि के ऊपर गुब्बारे की ऊँचाई ज्ञात कीजिए।
