Advertisements
Advertisements
प्रश्न
एक समतल भूमि पर खड़ी मीनार की छाया की उस समय की लंबाई जब सूर्य का उन्नयन कोण 30° है, उस समय की लंबाई से 50 m अधिक है जब सूर्य का उन्नयन कोण 60° था। मीनार की ऊँचाई ज्ञात कीजिए।
उत्तर
मान लीजिए कि SQ = h मीनार है।
∠SPQ = 30° और ∠SRQ = 60°
प्रश्न के अनुसार,
छाया की लंबाई 50 मीटर लंबी है, सूर्य का उन्नयन कोण 60 डिग्री की तुलना में 30 डिग्री है।
तो, PR = 50 m और RQ = x m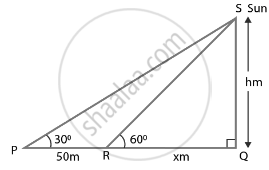
तो ∆SRQ में, हमारे पास है।
tan 60° = `"h"/x` ...`[∵ tan θ = "लंबवत"/"आधार" ⇒ tan 60^circ = "SQ"/"RQ"]`
⇒ `sqrt(3) = "h"/x` ...`[∵ tan 60^circ = sqrt(3)]`
⇒ ` x = "h"/sqrt(3)`
ΔSPQ में,
tan 30° = `"h"/(50 + x)` ...`[∵ tan 30^circ = "SQ"/"PQ" = "SQ"/("PR" + "PQ")]`
⇒ `1/sqrt(3) = "h"/(50 + x)` ...`[∵ tan 30^circ = 1/sqrt(3)]`
⇒ `50 + x = sqrt(3)"h"`
उपरोक्त समीकरण में x का मान प्रतिस्थापित करने पर, हमें प्राप्त होता है।
⇒ `50 + "h"/sqrt(3) = sqrt(3)"h"`
⇒ `(50sqrt(3) + "h")/sqrt(3) = sqrt(3)"h"`
⇒ `50sqrt(3) + "h" = 3"h"`
⇒ `50sqrt(3) = 3"h" - "h"`
⇒ `3"h" - "h" = 50sqrt(3)`
⇒ 2h = `50sqrt(3)`
⇒ h = `(50sqrt(3))/2`
⇒ h = `25sqrt(3)`
अतः, आवश्यक ऊंचाई `25sqrt(3) "m"` है।
APPEARS IN
संबंधित प्रश्न
सर्कस का एक कलाकार एक 20m लंबी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खंभे की ऊँचाई ज्ञात कीजिए।

भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
भूमि के एक बिंदु से एक 20 मीटर ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमश: 45° और 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
एक पेडस्टल के शिखर पर एक 1.6 मीटर ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बिच की दूरी ज्ञात कीजिए।
6 m ऊँचे एक खंभे की छाया भूमि पर `2sqrt3` m लंबी है। तब, उस समय सूर्य का उन्नयन कोण ______ है।
1.5 मीटर ऊँचाई वाला एक प्रेक्षक 22 मीटर ऊँची एक मीनार से 20.5 मीटर की दूरी पर खड़ा है। प्रेक्षक की आँख से मीनार की चोटी का उन्नयन कोण निर्धारित कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
किसी मकान की खिड़की भूमि से h m की ऊँचाई पर है। इस खिड़की से, सड़क के दूसरी ओर स्थित एक अन्य मकान के शिखर और आधार के क्रमशः उन्नयन और अवनमन कोण α और β पाए जाते हैं। सिद्ध कीजिए कि दूसरे मकान की ऊँचाई h(1 + tan α cot β) मीटर है।
