Advertisements
Advertisements
प्रश्न
किसी मकान की खिड़की भूमि से h m की ऊँचाई पर है। इस खिड़की से, सड़क के दूसरी ओर स्थित एक अन्य मकान के शिखर और आधार के क्रमशः उन्नयन और अवनमन कोण α और β पाए जाते हैं। सिद्ध कीजिए कि दूसरे मकान की ऊँचाई h(1 + tan α cot β) मीटर है।
उत्तर
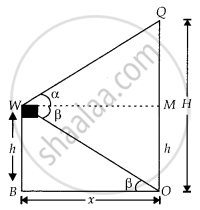
मान लीजिए दूसरे घर की ऊंचाई = OQ = Hm और OB = MW = xm है।
दिया गया है, पहले घर की ऊंचाई = WB = h = MO
और ∠QWM = α, ∠OWM = β = ∠WOB ...[वैकल्पिक कोण]
अब, ∆WOB,
tan β = `"WB"/"OB" = "h"/x`
⇒ x = `"h"/(tan β)` ...(i)
और ΔQWM में,
tan α = `"QM"/"WM"`
= `("OQ" - "MO")/"WM"`
⇒ tan α = `("H" - "h")/x`
⇒ x = `("H" - "h")/(tan α)` ...(ii)
समीकरण (i) और (ii) से, हम पाते हैं।
`"h"/(tan β) = ("H" - "h")/(tan α)`
⇒ h tan α = (H – h)tan β
⇒ h tan α = H tan β – h tan β
⇒ H tan β = h(tan α + tan β)
⇒ H = `"h"((tan α + tan β)/ tan β)`
⇒ H = `"h"(1 + tan α * 1/tan β)` ...`[∵ cot θ = 1/tan θ]`
= h(1 + tan α · cot β)
अतः, दूसरे घर की आवश्यक ऊँचाई h(1 + tanα · cotβ) है।
APPEARS IN
संबंधित प्रश्न
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
एक पेडस्टल के शिखर पर एक 1.6 मीटर ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो की मीनार के पाद की ओर एक समान चाल से जाता है। छ: सेकेंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
यदि एक मीनार की छाया की लंबाई बढ़ रही है, तो सूर्य का उन्नयन कोण भी बढ़ रहा है।
किसी मीनार की चोटी का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दुगुनी हो जाए, तो इसकी चोटी का उन्नयन कोण भी दुगुना हो जाएगा।
यदि एक मीनार की ऊँचाई तथा उसके आधार से प्रेक्षण बिंदु की दूरी दोनों ही 10% बढ़ जाते हैं, तो चोटी का उन्नयन कोण वही रहता है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
h ऊँचाई की किसी मीनार की चोटी से दो वस्तुओं, जो मीनार के आधार वाली रेखा में स्थित हैं, के अवनमन कोण α और β (β > α) हैं। दोनों वस्तुओं के बीच की दूरी ज्ञात कीजिए।
किसी मकान की निचली खिड़की भूमि से 2 m की ऊँचाई पर है तथा उसकी ऊपरी खिड़की निचली खिड़की से ऊर्ध्वाधरत : 4 m ऊपर है। किसी क्षण इन खिड़कियों से एक गुब्बारे के उन्नयन कोण क्रमश : 60° और 30° प्रेक्षित किए गए। भूमि के ऊपर गुब्बारे की ऊँचाई ज्ञात कीजिए।
