Question

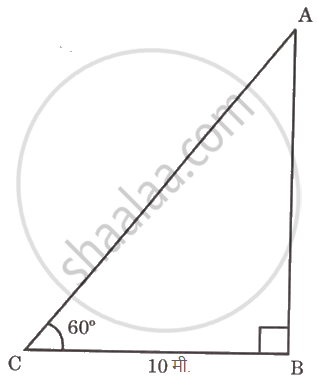
किसी पेड़ के तने से 10 मी. की दूरी पर खड़ा निरीक्षक पेड़ की चोटी की ओर देखता है तब 60° माप का उन्नत कोण बनता है। तो उस पेड़ की ऊँचाई ज्ञात करने के लिए निम्न कृति पूर्ण कीजिए। `(sqrt3 = 1.73)`

कृति:

ऊपर दी गई आकृति में, बिंदु C के पास निरीक्षक है और AB पेड़ है। AB = h = पेड़ की ऊँचाई, निरीक्षक की पेड़ से दूरी BC = 10 मी.

उन्नत कोण (θ) = BCA= 60°

tan θ = `square/("BC")`  ...(I)

tan 60° = `square`  ...(II)

`("AB")/("BC") = sqrt3`  ...((I) तथा (II) से)

AB = BC × `sqrt3` = `10sqrt3`

AB = 10 × 1.73 = `square`

∴ पेड़ की ऊँचाई `square` मी. है।

Answer 1

ऊपर दी गई आकृति में, बिंदु C के पास निरीक्षक है और AB पेड़ है। AB = h = पेड़ की ऊँचाई, निरीक्षक की पेड़ से दूरी BC 10 मी.

उन्नत कोण (θ) = BCA= 60°

tan θ = \[\frac{\boxed{\text{AB}}}{\text{BC}}\]  ...(I)

tan 60° = \[\boxed{\sqrt{3}}\]  ...(II)

`("AB")/("BC") = sqrt3`  ...((I) तथा (II) से)

AB = BC × `sqrt3` = `10sqrt3`

AB = 10 × 1.73 = \[\boxed{17.3}\]

∴ पेड़ की ऊँचाई \[\boxed{17.3}\] मी. है।