Question

कोई लड़ाकू जहाज 1.5 km की ऊंचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है। ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600 ms^-1 की चाल से दागा गया गोला वायुयान पर वार कर सके। वायुयान के चालक को किस न्यूनतम ऊंचाई पर जहाज को उड़ाना चाहिए जिससे गोली लगने से बच सके। (g = 10 ms^-2)

Answer 1

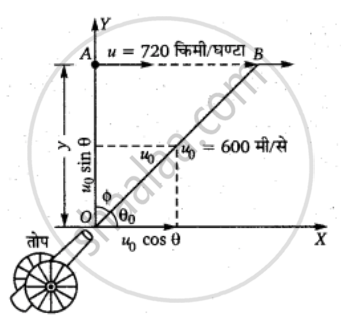
लड़ाकू जहाज की ऊँचाई,

y = 1.5 किमी = 1500 मी

लड़ाकू जहाज की चाल,

u = 720 किमी/घंटा

= `(720 xx 5/18)` मी/से

= 200 मी/से  (क्षैतिज दिशा अर्थात X - दिशा में)

तोप से दागे गए गोले की चाल, u₀ = 600 मी/से^-1

माना गोले के वेग `vec"u"_0` की दिशा क्षैतिज से θ₀ कोण पर है।

माना O पर तोप से दागा गया गोला इसके ठीक ऊपर लड़ाकू जहाज की स्थिति A से t सेकंड में जहाज की स्थिति B में पहुंचने पर वार करता है। अतः जहाज द्वारा चली क्षैतिज दूरी = गोले का क्षैतिज दिशा में विस्थापन

∴ `"u" xx "t" = "ν"_0  "cos"  theta_0 xx "t"`

अथवा `"cos"  theta_0 = "u"/"u"_0 = (200  "मी"//"से")/(600  "मी"//"से") = 1/3 = 0.3333`

∴ `theta_ 0 = "cos"^-1 (0.3333) = 70.5^circ`

अतः ऊर्ध्वाधर से तोप की नाल का कोण

θ = 90° - θ₀ = 90°- 70.5° = 19.5°

गोले के वार से बचने के लिए वायुयान चालक को वायुयान को गोले द्वारा Y दिशा में प्राप्त अधिकतम ऊंचाई पर उड़ाना चाहिए। यही इसकी न्यूनतम ऊंचाई होगी।

अतः न्यूनतम ऊंचाई,

`"H"_"M" = ("u"_0^2  "sin"^2  theta_0)/(2"g") = ("u"_0^2 (1 - "cos"^2  theta_0))/(2"g")` 

= `((600)^2 xx [1 - (1//3)^2])/(2 xx 10)`

= 16000 मी = 16 किमी