Advertisements
Advertisements
Question
Light falls from glass (μ = 1.5) to air. Find the angle of incidence for which the angle of deviation is 90°.
Solution
Given,
Light falls from glass to air.
Refractive index (μ) of glass = 1.5
Critical angle (θc)
\[= \sin^{- 1} \left( \frac{1}{\mu} \right)\]
\[= \sin^{- 1} \left( \frac{1}{1 . 5} \right) = 41 . 80\]
We know that the maximum attainable angle of deviation in refraction is (90° − 41.8°)
= 47.2°
In this case, total internal reflection must have taken place.
In reflection,
Deviation = 180° − 2i = 90°
⇒ 2i = 90°
⇒ i = 45°
Hence, the required angle of incidence is 45°.
APPEARS IN
RELATED QUESTIONS
Give a scientific reason:
Danger signals are red in colour.
Name the phenomenon responsible for it.
Why does unpolarised light from a source show a variation in intensity when viewed through a polaroid which is rotated?
The image formed by a concave mirror
A concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
A concave mirror forms an image of 20 cm high object on a screen placed 5.0 m away from the mirror. The height of the image is 50 cm. Find the focal length of the mirror and the distance between the mirror and the object.
A 1 cm object is placed perpendicular to the principal axis of a convex mirror of focal length 7.5 cm. Find its distance from the mirror if the image formed is 0.6 cm in size.
A point source S is placed midway between two converging mirrors having equal focal length f as shown in figure. Find the values of d for which only one image is formed.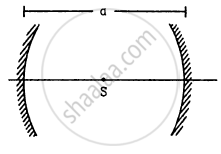
k transparent slabs are arranged one over another. The refractive indices of the slabs are μ1, μ2, μ3, ... μk and the thicknesses are t1 t2, t3, ... tk. An object is seen through this combination with nearly perpendicular light. Find the equivalent refractive index of the system which will allow the image to be formed at the same place.
Light is incident from glass (μ = 1.50) to water (μ = 1.33). Find the range of the angle of deviation for which there are two angles of incidence.
A point source is placed at a depth h below the surface of water (refractive index = μ). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
A biconvex thick lens is constructed with glass (μ = 1.50). Each of the surfaces has a radius of 10 cm and the thickness at the middle is 5 cm. Locate the image of an object placed far away from the lens.
One end of a cylindrical glass rod (μ = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (μ = 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
A paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer?
Answer the following question in detail.
State the conditions under which a rainbow can be seen.
Pick the wrong answer in the context with rainbow.
Rainbow is the phenomenon due to ______.
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is ______.
