Advertisements
Advertisements
Question
A paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer?
Solution
Given:
Radius of the paperweight (R) = 3 cm
Refractive index of the paperweight (μ2) = 3/2
Refractive index of the air (μ1) = 1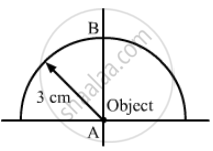
In the first case, the refraction is at A.
u = 0 and R = ∞
We know:
\[\frac{\mu_2}{v} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\]
\[ \Rightarrow \frac{\frac{3}{2}}{v} - \frac{1}{0} = \frac{\mu_2 - \mu_1}{\infty}\]
\[ \Rightarrow v = 0\]
Therefore, the image of the letter is formed at the point.
For the second case, refraction is at point B.
Here,
Object distance, u = −3 cm
R = − 3 cm
μ1 = 3/2
μ2 = 1
Thus, we have:
\[\frac{\mu_2}{v} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\]
\[\frac{1}{v} - \frac{3}{2 \times ( - 3)} = \frac{1 - \frac{3}{2}}{- 3}\]
\[ \Rightarrow \frac{1}{v} + \frac{3}{2 \times 3} = \frac{1}{6}\]
\[ \Rightarrow \frac{1}{v} = \frac{1}{6} - \frac{1}{2}\]
\[ \Rightarrow v = - 3 \text{ cm }\]
Hence, there will be no shift in the final image.
APPEARS IN
RELATED QUESTIONS
Why does unpolarised light from a source show a variation in intensity when viewed through a polaroid which is rotated?
Draw the intensity distribution for the diffraction bands produced due to single slit ?
Why does the Sun look reddish at sunset or sunrise ?
In the meterbridge experimental set up, shown in the figure, the null point ‘D’ is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD = 60 cm. Calculate the values of R1 and R2.
The image formed by a concave mirror
A 3 cm tall object is placed at a distance of 7.5 cm from a convex mirror of focal length 6 cm. Find the location, size and nature of the image.
A point source S is placed midway between two converging mirrors having equal focal length f as shown in figure. Find the values of d for which only one image is formed.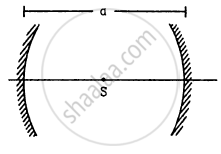
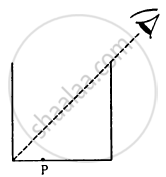
Locate the image of the point P as seen by the eye in the figure.

k transparent slabs are arranged one over another. The refractive indices of the slabs are μ1, μ2, μ3, ... μk and the thicknesses are t1 t2, t3, ... tk. An object is seen through this combination with nearly perpendicular light. Find the equivalent refractive index of the system which will allow the image to be formed at the same place.
A cylindrical vessel, whose diameter and height both are equal to 30 cm, is placed on a horizontal surface and a small particle P is placed in it at a distance of 5.0 cm from the centre. An eye is placed at a position such that the edge of the bottom is just visible (see figure). The particle P is in the plane of drawing. Up to what minimum height should water be poured in the vessel to make the particle P visible?
A point source is placed at a depth h below the surface of water (refractive index = μ). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water = 4/3.
Answer the following question in detail.
Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
State any one difference between a primary rainbow and a secondary rainbow.
Explain the formation of primary and secondary rainbow.
A parallel beam of light of wavelength 5890 Å falls normally on a slit of width 0.2 mm. Find the distance between the first minima on the two sides of the central maximum of the diffraction pattern observed on a screen placed in the focal plane of a convex lens of focal length 50 cm. The lens is placed quite close to the slit.
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question : |
In an optical fibre, if n1 and n2 are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
The sky would appear red instead of blue if
