Advertisements
Advertisements
Question
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water = 4/3.
Solution
Given,
Height (h) of the water in the container = 20 cm
Ceiling of the room is 2.0 m above the water surface.
Radius of the rubber ring = r
Refractive index of water = 4/3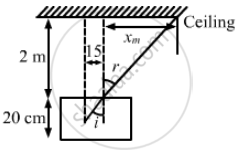
From the figure, we can infer:
\[\sin i = \frac{15}{25}\]
Using Snell's law, we get:
\[\frac{\sin i}{\sin r} = \frac{1}{\mu} = \frac{3}{4}\]
\[ \Rightarrow \sin i = \frac{4}{5}\]
From the figure, we have:
\[So, \]
\[\sin r = \frac{\tan r}{\sqrt{1 + \tan^2 r}}\]
\[ = \frac{\frac{x}{2}}{\sqrt{1 + \frac{x^2}{4}}}\]
\[ \Rightarrow \frac{x}{\sqrt{4 + x^2}} = \frac{4}{5}\]
\[\Rightarrow 25 x^2 = 16(4 + x^2 )\]
\[ \Rightarrow 9 x^2 = 64\]
\[ \Rightarrow x = \frac{8}{3} m\]
Total radius of the shadow = \[\frac{8}{3} + 0 . 15 = 2 . 81 m\]
(b)
Condition for the maximum value of r:
Angle of incidence should be equal to the critical angle, i.e., \[i = \theta_c\]
Let us take R as the maximum radius.
Now,
\[\sin \theta_c = \frac{\sin \theta_c}{\sin r}\]
\[ = \frac{R}{\sqrt{R^2 + 20}} = \frac{3}{4} (\sin r = 1)\]
\[ \Rightarrow 16 R^2 = 9 R^2 + 9 \times 400\]
\[ \Rightarrow 7 R^2 = 9 R^2 + 9 \times 400\]
\[ \Rightarrow R = 22 . 67 cm\]
APPEARS IN
RELATED QUESTIONS
Fill in the blank:
Very fine particles mainly scatter ………… colored light.
Draw the intensity distribution for the diffraction bands produced due to single slit ?
Why does the Sun look reddish at sunset or sunrise ?
The image formed by a concave mirror
A thin lens is made with a material having refractive index
\[\mu = 1 \cdot 5\]. Both the side are convex. It is dipped in water \[\mu = 1 \cdot 33\]. It will behave like
A convex lens is made of a material having refractive index
\[1 \cdot 2\] Both the surfaces of the lens are convex. If it is dipped into water (μ = 1.33), it will behave like
A concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
A 3 cm tall object is placed at a distance of 7.5 cm from a convex mirror of focal length 6 cm. Find the location, size and nature of the image.
A point source is placed at a depth h below the surface of water (refractive index = μ). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
The diameter of the sun is 1.4 × 109 m and its distance from the earth is 1.5 × 1011 m. Find the radius of the image of the sun formed by a lens of focal length 20 cm.
Fill in the blank and rewrite the completed statement:
Very fine particles mainly scatter ______ light.
Answer the following question in detail.
State the conditions under which a rainbow can be seen.
Answer the following question in detail.
Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
State any one difference between a primary rainbow and a secondary rainbow.
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question: |
A diamond is immersed in such a liquid which has its refractive index with respect to air as greater than the refractive index of water with respect to air. Then the critical angle of diamond-liquid interface as compared to critical angle of diamond-water interface will
A passenger in an aeroplane shall ______.
Between the primary and secondary rainbows, there is a dark band known as Alexandar’s dark band. This is because ______.
- light scattered into this region interfere destructively.
- there is no light scattered into this region.
- light is absorbed in this region.
- angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
