Question

A paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer?

Answer 1

Given:
Radius of the paperweight (R) = 3 cm
Refractive index of the paperweight (μ₂) = 3/2
Refractive index of the air (μ₁) = 1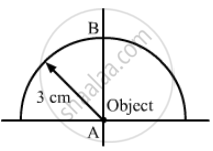

In the first case, the refraction is at A.
u = 0 and R = ∞
We know:

\[\frac{\mu_2}{v} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\] 

\[ \Rightarrow \frac{\frac{3}{2}}{v} - \frac{1}{0} = \frac{\mu_2 - \mu_1}{\infty}\] 

\[ \Rightarrow v = 0\]
Therefore, the image of the letter is formed at the point.
For the second case, refraction is at point B.
Here,
Object distance, u = −3 cm
R = − 3 cm
μ₁ = 3/2
μ₂ = 1
Thus, we have:

\[\frac{\mu_2}{v} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}\] 

\[\frac{1}{v} - \frac{3}{2 \times ( - 3)} = \frac{1 - \frac{3}{2}}{- 3}\] 

\[ \Rightarrow \frac{1}{v} + \frac{3}{2 \times 3} = \frac{1}{6}\] 

\[ \Rightarrow \frac{1}{v} = \frac{1}{6} - \frac{1}{2}\] 

\[ \Rightarrow v =  - 3  \text{ cm }\]
Hence, there will be no shift in the final image.