Advertisements
Advertisements
प्रश्न
A candle flame 1.6 cm high is imaged in a ball bearing of diameter 0.4 cm. If the ball bearing is 20 cm away from the flame, find the location and the height of the image.
Advertisements
उत्तर
Given,
Height (h1) of the candle flame taken as object AB = 1.6 cm
Diameter of the ball bearing (d) = 0.4 cm
So, radius = 0.2 cm
Distance of object, u = 20 cm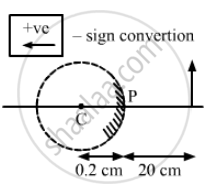
Using mirror formula,
\[\frac{1}{v} + \frac{1}{u} = \frac{2}{R}\]
Putting the values according to sign conventions, we get,
\[\frac{1}{( - 20)} + \frac{1}{v} = \frac{2}{0 . 2}\]
\[ \Rightarrow \frac{1}{v} = \frac{1}{20} + 10\]
\[ \Rightarrow v = 0 . 1 cm or 1 . 0 \text{ mm inside the ball bearing . }\]
\[Magnification = m\]
\[ = \frac{A'B'}{AB} = - \frac{v}{u} = m\]
\[ = \frac{A'B'}{200} = \frac{1}{200}\]
\[\Rightarrow A'B'=\frac{AB}{200}=+\frac{1 . 6}{200} = + 0 . 08 \text{ cm } (+0008\text{ cm })\]
Hence, the distance of the image is 1 cm.
Height of the image is 0.008 cm.
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Very fine particles mainly scatter ………… colored light.
Why can’t we see clearly through fog?
Draw the intensity distribution for the fringes produced in interference ?
Draw the intensity distribution for the diffraction bands produced due to single slit ?
In the meterbridge experimental set up, shown in the figure, the null point ‘D’ is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD = 60 cm. Calculate the values of R1 and R2.
Suppose you are inside the water in a swimming pool near an edge. A friends is standing on the edge. Do you find your friend taller or shorter than his usual height?
A convex lens is made of a material having refractive index
\[1 \cdot 2\] Both the surfaces of the lens are convex. If it is dipped into water (μ = 1.33), it will behave like
A concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
A 3 cm tall object is placed at a distance of 7.5 cm from a convex mirror of focal length 6 cm. Find the location, size and nature of the image.
k transparent slabs are arranged one over another. The refractive indices of the slabs are μ1, μ2, μ3, ... μk and the thicknesses are t1 t2, t3, ... tk. An object is seen through this combination with nearly perpendicular light. Find the equivalent refractive index of the system which will allow the image to be formed at the same place.
An optical fibre (μ = 1.72) is surrounded by a glass coating (μ = 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
One end of a cylindrical glass rod (μ = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (μ = 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
Fill in the blank and rewrite the completed statement:
Very fine particles mainly scatter ______ light.
Answer the following question in detail.
Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
Pick the wrong answer in the context with rainbow.
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question : |
In an optical fibre, if n1 and n2 are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
| Case study: Mirage in deserts |
|
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question: |
The following figure shows a cross-section of a ‘light pipe’ made of a glass fiber of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for the following phenomena to occur.
Between the primary and secondary rainbows, there is a dark band known as Alexandar’s dark band. This is because ______.
- light scattered into this region interfere destructively.
- there is no light scattered into this region.
- light is absorbed in this region.
- angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
