Advertisements
Advertisements
प्रश्न
A concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
उत्तर
Using sign conventions, given,
Focal length of the concave mirror:
f = −20 cm
As per the question,
Magnification (m) is:
\[m = - \frac{v}{u} = 2\]
⇒ v = −2u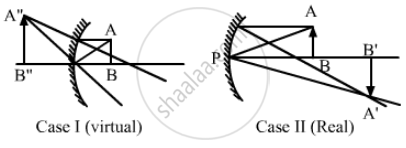
Case I (Virtual image):
Using mirror formula,
\[\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow - \frac{1}{2u} - \frac{1}{u} = \frac{1}{f}\]
\[ \Rightarrow \frac{3}{2u} = \frac{1}{f}\]
\[ \Rightarrow u = \frac{3f}{2} = 30 \text{ cm }\]
Hence, the required positions of objects are 10 cm or 30 cm from the concave mirror.
APPEARS IN
संबंधित प्रश्न
Name the phenomenon responsible for it.
Why does unpolarised light from a source show a variation in intensity when viewed through a polaroid which is rotated?
In the meterbridge experimental set up, shown in the figure, the null point ‘D’ is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD = 60 cm. Calculate the values of R1 and R2.
The image formed by a concave mirror
A convex lens is made of a material having refractive index
\[1 \cdot 2\] Both the surfaces of the lens are convex. If it is dipped into water (μ = 1.33), it will behave like
A concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
A point source S is placed midway between two converging mirrors having equal focal length f as shown in figure. Find the values of d for which only one image is formed.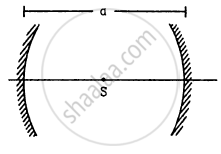
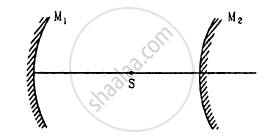
A converging mirror M1, a point source S and a diverging mirror M2 are arranged as shown in figure. The source is placed at a distance of 30 cm from M1. The focal length of each of the mirrors is 20 cm. Consider only the images formed by a maximum of two reflections. It is found that one image is formed on the source itself. (a) Find the distance between the two mirrors. (b) Find the location of the image formed by the single reflection from M2.
An optical fibre (μ = 1.72) is surrounded by a glass coating (μ = 1.50). Find the critical angle for total internal reflection at the fibre-glass interface.
Light is incident from glass (μ = 1.50) to water (μ = 1.33). Find the range of the angle of deviation for which there are two angles of incidence.
A point source is placed at a depth h below the surface of water (refractive index = μ). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water = 4/3.
Fill in the blank and rewrite the completed statement:
Very fine particles mainly scatter ______ light.
Answer the following question in detail.
Explain the formation of a primary rainbow. For which angular range with the horizontal is it visible?
A plano-convex lens is made of material having refractive index 1.5. The radius of curvature of curved surface is 40 cm. The focal length of the lens is ____________ cm.
Explain the formation of primary and secondary rainbow.
A passenger in an aeroplane shall ______.
