Advertisements
Advertisements
Question
Multiple choice question :
Let f and g be two function given by f = {(0, 1), (2, 0), (3, – 4), (4, 2), (5, 7)} g = {(0, 2), (1, 0), (2, 4), (– 4, 2), (7, 0) then the range of fog is
Options
{0, 2, 3, 4, 5}
{– 4, 1, 0, 2, 7}
{1, 2, 3, 4, 5}
{0, 1, 2}
Solution
{0, 1, 2}
Explanation;
f = {(0, 1) (2, 0) (3, – 4) (4, 2) (5, 7)}
g = {(0, 2) (1, 0) (2, 4) (– 4, 2) (7, 0)}
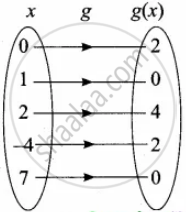
fog = f[g(x)]
f[g(0)] = f(2) = 0
f[g(1)] = f(0) = 1
f[g(2)] = f(4) = 2
f[g(– 4)] = f(2) = 0
f[g(7)] = f(0) = 1
Range of fog = {0, 1, 2}
APPEARS IN
RELATED QUESTIONS
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = x – 6, g(x) = x2
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = `(2)/x`, g(x) = 2x2 – 1
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = `(x + 6)/3`, g(x) = 3 – x
Using the function f and g given below, find fog and gof. Check whether fog = gof
f(x) = 3 + x, g(x) = x – 4
If f(x) = x2 – 1, g(x) = x – 2 find a, if gof(a) = 1
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x – 1, g(x) = 3x + 1 and h(x) = x2
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x2, g(x) = 2x and h(x) = x + 4
Consider the function f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh)
f(x) = x – 4, g(x) = x2 and h(x) = 3x – 5
Multiple choice question :
If g = {(1, 1), (2, 3), (3, 5), (4, 7)} is a function given by g(x) = αx + β then the value of α and β are
If f(x)= x2, g(x) = 3x and h(x) = x – 2 Prove that (fog)oh = fo(goh)
