Question

Multiple choice question : 

Let f and g be two function given by  f = {(0, 1), (2, 0), (3, – 4), (4, 2), (5, 7)} g = {(0, 2), (1, 0), (2, 4), (– 4, 2), (7, 0) then the range of fog is

पर्याय

• {0, 2, 3, 4, 5}

• {– 4, 1, 0, 2, 7}

• {1, 2, 3, 4, 5}

• {0, 1, 2}

Answer 1

{0, 1, 2}

Explanation;

f = {(0, 1) (2, 0) (3, – 4) (4, 2) (5, 7)}

g = {(0, 2) (1, 0) (2, 4) (– 4, 2) (7, 0)}

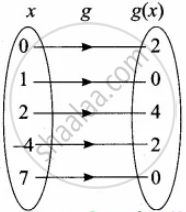
fog = f[g(x)]

f[g(0)] = f(2) = 0

f[g(1)] = f(0) = 1

f[g(2)] = f(4) = 2

f[g(– 4)] = f(2) = 0

f[g(7)] = f(0) = 1

Range of fog = {0, 1, 2}